Hoe lang moet een roerhoorntje zijn?
Overal lees je aanbevelingen hoe je optimaal stuurvlakken aan servo's koppelt: "gebruik het binnenste oogje van de servohevel en maak het roerhoorntje zo groot mogelijk. Zo gebruik je de volle uitslag van de servo en heb je de meest nauwkeurige aansturing".
Ja, da's makkeljk, maar... wat is "zo groot mogelijk"? Haal je dan de volle uitslag wel?
Laten we dit eens wetenschappelijk benaderen. Als je de maximale weg die de stuurstang aflegt weet en je weet de grootte en de maximale uitslag van een stuurvlak dan kun je toch gewoon de lengte van je roerhoorntje berekenen? Mijn meetkunde kennis van de middelbare school is wat roestig, maar niet verdwenen. Aan de slag dus.
Allereerst maken we een schematische tekening van de situatie:
Hierbij is:
Als je hier even middelbare school-wiskunde op loslaat kom ik op de volgende formule voor h:
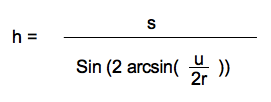
Oeps, da's wel erg moeilijk. Niet zo makkelijk effe op de bouwplank uit te rekenen.
Kunnen we misschien een versimpeling toepassen? Eens even kijken.
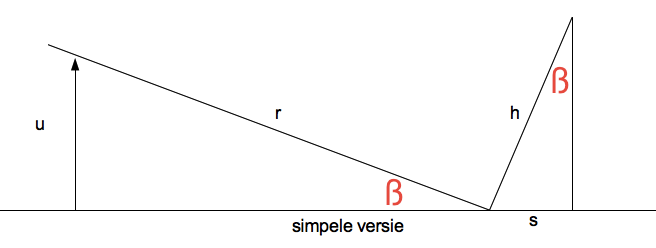
Zoiets? De maximale roeruitslag heb ik nu haaks op de nullijn gezet. Volgens mij maakt dat niet zo heel veel uit. De 2 driehoeken die je nu ziet zijn gelijkvormig. Alleen de grootte verschilt. Nu kun je heel eenvoudig h berekenen:
Kijk! Da's werkbaar!
We kunnen nu dus stellen: :teacher:
De lengte van een roerhoorntje wordt berekend door de lengte van het stuurvlak te vermenigvuldigen met de maximale uitslag van de servo en dit te delen door de maximale uitslag van het stuurvlak
Ook wel genoemd, de formule van Wubbe
Veel plezier ermee!
Overal lees je aanbevelingen hoe je optimaal stuurvlakken aan servo's koppelt: "gebruik het binnenste oogje van de servohevel en maak het roerhoorntje zo groot mogelijk. Zo gebruik je de volle uitslag van de servo en heb je de meest nauwkeurige aansturing".
Ja, da's makkeljk, maar... wat is "zo groot mogelijk"? Haal je dan de volle uitslag wel?
Laten we dit eens wetenschappelijk benaderen. Als je de maximale weg die de stuurstang aflegt weet en je weet de grootte en de maximale uitslag van een stuurvlak dan kun je toch gewoon de lengte van je roerhoorntje berekenen? Mijn meetkunde kennis van de middelbare school is wat roestig, maar niet verdwenen. Aan de slag dus.
Allereerst maken we een schematische tekening van de situatie:
Hierbij is:
- s = de maximale weg (één kant op) die de stuurstang aflegt. Da's aan de servo gewoon op te meten
- r = de lengte van het stuurvlak
- u = de aanbevolen maximale uitslag van het stuurvlak. Vaak staat dit in de handleiding van het toestel
- h = de berekende lengte van het roerhoorntje
Als je hier even middelbare school-wiskunde op loslaat kom ik op de volgende formule voor h:
Oeps, da's wel erg moeilijk. Niet zo makkelijk effe op de bouwplank uit te rekenen.
Kunnen we misschien een versimpeling toepassen? Eens even kijken.
Zoiets? De maximale roeruitslag heb ik nu haaks op de nullijn gezet. Volgens mij maakt dat niet zo heel veel uit. De 2 driehoeken die je nu ziet zijn gelijkvormig. Alleen de grootte verschilt. Nu kun je heel eenvoudig h berekenen:
Kijk! Da's werkbaar!
We kunnen nu dus stellen: :teacher:
De lengte van een roerhoorntje wordt berekend door de lengte van het stuurvlak te vermenigvuldigen met de maximale uitslag van de servo en dit te delen door de maximale uitslag van het stuurvlak
Ook wel genoemd, de formule van Wubbe
Veel plezier ermee!
Laatst bewerkt door een moderator:
) programma waarin je van een paar honderd servo's de WERKELIJKE prestaties zien. En die wijken soms wel 50% van wat de fabrikant in de folder heeft gezet .....