houtjesplakker
PH-SAM
Rick, bedankt voor je uitleg. Het is nu helder waarom dit zo is. Dat dit ook zo is bij een kruisstaart is ook duidelijk, maar de ervaring van het weekend was anders.
Follow along with the video below to see how to install our site as a web app on your home screen.
Nota: This feature may not be available in some browsers.
Bij het herlezen van je uitleg is het mij niet duidelijk dat de "rol" meewerkt. Wanneer op de rug gevlogen wordt staan de roeren bij rechtsom sturen naar links (van achter gezien) hetgeen een linksom koppel genereert. Wanneer model voorzien is van een "omgekeerde" V staart werkt de rol beweging wel mee.
Toch? Of maak ik nu ergens een denk fout?
Klopt. Ik heb er ook nooit wat van gemerkt.
Overigens moet een gewoon verticaal kielvak met Ri-roer ook een rol-effect genereren. Het steekt immers assymetrisch uit boven de rol-as. Tenzij het kielvlak symmetrisch naar onderen uitsteekt, zoals bij moderne DLG's. Maar ook van zo'n assymmetrisch vertikaal kielvlak heb ik nooit ook maar het minste rol-effect opgemerkt. Terwijl ik wel heel duidelijk merk dat zo'n vertikaal kielvlak + horizontaal stabilo veel preciezer en directer stuurt dan een V-staart.
In theorie is het rol-effect aanwezig, in de praktijk merkt niemand het.
Dirk.
Schitterend zichtbaar. Vooral ook het torderen van de stabilo-vlakken tijdens de lierstart, als de snelheid, en dus de krachten, groot zijn.Begrijp me goed, ik zeg niet dat het er niet is. Maar wel dat ik het onder het vliegen niet op kan merken. Wel ZIEN trouwens. Filmpje van mijn Brillant waar het griezelig goed zichtbaar is:
Tut tut tut tut!Wat me wel kan verbazen is dat men er bij een v-staart over begint terwijl het er bij een normaal kielvlak met richtingsroer ook is, en daar hoor je niemand over....
Ik was de eerste!DirkSchipper zei:Overigens moet een gewoon verticaal kielvak met Ri-roer ook een rol-effect genereren. Het steekt immers assymetrisch uit boven de rol-as. Tenzij het kielvlak symmetrisch naar onderen uitsteekt, ...
Iedere V-staart geeft een rolroer effect
hehe, het was ook niet tegen jou bedoeldEr zijn nog meer lezers
Maar in draadjes over v-staarten kom je dit iedere keer tegen alsof het iets typisch voor die constructie zou zijn.
Hoi Rick,
Ik bestrijdt het helemaal niet. Een rekenvoorbeeld mag, maar de torsie in de staart van mijn Brillant maakt het wat mij betreft aanschouwelijk genoeg.
Blijft staan dat ik het niet merk onder het vliegen.
.
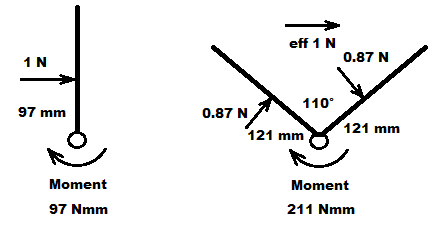
Maar goed, dit draagt verder niet echt bij aan de discussie. Ik hoop alleen dat het een ieder duidelijk is dat dit volgens mij niet "een nadeel van een v-staart" is.
Bij slankheden van 8 of minder is e.e.a. wel degelijk merkbaar en daar heeft een omgekeerde V dus een voordeeltje.
Volgens mij bedoelt Rick de slankheid va de hoofdvleugel. Hoe groter diens slankheid, hoe minder je van het rol-moment van de (V-)staart zult merken.Bedoel je niet "slankheid hoger dan 8"? Bij steeds hogere slankheid grijpt de kracht steeds verder uit de rompas aan, en wordt het rolmoment dus groter?
Volgens mij bedoelt Rick de slankheid va de hoofdvleugel. Hoe groter diens slankheid, hoe minder je van het rol-moment van de (V-)staart zult merken.
Dirk
Nu benader je het probleem door te veronderstellen dat je daadwerkelijk 1N op weet te wekken.
Om die 1N op te kunnen wekken moet je:
- voldoende vliegsnelheid hebben.
- voldoende oppervlakte aanwezig.
Neem 1 identieke vleugel/massa, met kruis en V-staart, volgt dat de vliegsnelheid gelijk is. Dan is uit jouw rekenvoorbeeld vast te stellen dat je dus never nooit uitkomt met het overnemen van een geprojecteerd oppervlak.
In dit draadje wordt verwezen naar: Charles River Radio Controllers - Quick V-Tail Sizing
Hierin staan aannamen(?) en formules tegen die vraagtekens oproepen.
Wie kan deze nader uitleggen?
Avt = Ah + Av
Ah = Avt [cos(angle)]^2
Av = Avt [sin(angle)]^2
Angle = artan (Av / Ah)^1/2
