Voor mijn profielwerkstuk ben ik bezig een soort introductie tot aerodynamica en enkele belangrijke dingen zoals stabiliteit te schrijven. Het leek me leuk om delen daarvan in artikelvorm hier neer te zetten zodat iedereen er wat aan heeft.
Dit deel gaat over stabiliteit. In andere woorden, wat het verschil is tussen een blaadje papier en jouw vliegtuig. Ik heb geprobeerd het zo overzichtelijk mogelijk te houden en alles zo duidelijk mogelijk uit te leggen. De terminologie heb ik ook zo simpel mogelijk gehouden. Alle tips ter verbetering zijn natuurlijk welkom, bijvoorbeeld qua duidelijkheid. Ik krijg er een punt voor dus misschien help je me wel aan een hoger punt.
De afbeeldingen zijn in het Engels aangezien ik van plan ben dit ook daarin te vertalen. Schrik niet van die paar formules, er zit zo weinig mogelijk wiskunde in.
[size=+2]Stabiliteit[/size]
De basis
Een vleugelprofiel genereert lift door de lucht af te buigen. De over- of onderdruk rond een vleugelprofiel trekt en duwt als het ware aan het profiel, loodrecht op het stukje waar de betreffende druk op duwt. Alle kleine stukjes trek- en duwkracht bij elkaar opgeteld zorgen ervoor dat een profiel een liftkracht opwekt. In de volgende afbeelding zijn de drukvectoren weergegeven: rood is een harde drukkracht, blauw andersom. Het profiel levert in deze situatie lift.

Maar stel nu dat de lift nul is: er is geen liftkracht. Dan zorgen alle trek- en duwkrachten ervoor dat het profiel toch nog een beetje om zijn as wil draaien. Dit noemen we het moment. Een symmetrisch profiel heeft bij nul lift geen moment: de krachten zijn immers overal in spiegelbeeld en zorgen er dus niet voor dat het profiel nog een kant op wil draaien.
Gaat het profiel nu lift leveren, zorgen alle trek- en duwkrachten voor een totale liftkracht. Deze kun je overal op het profiel meten, maar dan krijg je én een liftkracht én een momentkracht (hij draait om zijn as). Hier hebben we natuurlijk niks aan, daarom hebben we het 'Center of Pressure' (van nu af aan CoP) bedacht. Dit is het punt op het profiel waar bij een bepaalde invalshoek de lift aangrijpt, zonder momentkracht. Als je het profiel op dit punt bij een bepaalde invalhoek vast houdt, voel je dus alleen een kracht omhoog en geen draaikracht.
Dit punt blijft niet hetzelfde met invalshoek: het verschuift. Bij nul lift is er geen liftkracht, dus als het profiel met zijn neus omlaag wil kantelen ligt het CoP oneindig ver achter het profiel en is hij ook oneindig klein: er is immers geen lift.
Om profielen te kunnen vergelijken is er de 'Momentcoëfficiënt' (vanaf nu Cm). De formule daarvoor is:
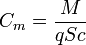
M is daarbij de momentkracht, S het vleugeloppervlak, c de koorde en q de dynamische druk. Het vleugeloppervlak en de koorde blijven bij een vliegtuig natuurlijk constant, deze kunnen we even weglaten. De dynamische druk q is nauw verwant met de kinetische energie van een deeltje (je weet wel, ½mv2) en dit is de formule ervoor:
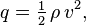
Waarbij p (rho) de luchtdichtheid is (op zeeniveau 1,23) en v de snelheid.
We meten de momentcoëfficiënt altijd op 25% van de koorde. Het feit wil namelijk dat het momentcoëfficiënt nauwelijks verandert rond dit punt (het is het aerodynamisch middelpunt van het profiel). Dit is vooral zo bij dunne symmetrische profielen, het Cm fluctueert steeds meer naarmate het profiel dikker en minder symmetrisch wordt. We nemen even aan dat Cm constant is, hoewel hij in de praktijk toch iets verschuift met invalshoek, maar niet veel.
Als we de tweede formule bij de Cm formule leggen en stellen dat Cm constant is, zien we dat het totale moment kwadratisch toeneemt met de snelheid. De snelheid hangt samen met de invalshoek: hoe lager de invalshoek, hoe groter de snelheid. De lift blijft gelijk, dus de plek van het CoP moet verschuiven: anders kan er geen verandering in moment komen. We kunnen dus afleiden dat als het Cm negatief is, het moment ook altijd negatief is. Let op: we hebben afgesproken dat het moment (en dus Cm) negatief is als het profiel met zijn neus omlaag wil kantelen!
We weten nu dus dat met een negatief Cm het CoP naar achteren verschuift met hogere snelheid, dus lagere invalshoek.
We hebben 3 soorten profielen: die waarbij het Cm negatief is, die waarbij het Cm 0 is en die waarbij het Cm positief is. Symmetrische profielen hebben altijd een Cm van 0, maar we hebben ook profielen die niet symmetrisch zijn met een Cm van 0. We gaan nu eerst bekijken wat er bij deze verschillende soorten profielen met het CoP gebeurt met AOA (AOA = Angle Of Attack, invalshoek):

De pijl die de plaats van het CoP aangeeft is net zo groot als de liftcoëfficiënt. Is de pijl dus 4 keer zo klein, kun je 2 keer zo snel vliegen. De snelheid varieert en die pijl blijft dus bij een vliegtuig altijd even groot. Hij verschuift dus wel en verandert daarmee het punt waarop de lift van de vleugel aangrijpt.
Een stapje verder: hoe stabiliteit werkt
Als een vliegtuig een bepaalde invalshoek (dus snelheid) heeft, willen we dat het vliegtuig deze snelheid houdt. Krijgt het vliegtuig een iets andere invalshoek, willen we dat het vliegtuig zichzelf corrigeert en weer zijn oorspronkelijke invalshoek aanneemt.
Dat kunnen we op verschillende manieren realiseren, maar we bekijken het vliegtuig even als een geheel. Het heeft een bepaalde invalshoek, en in normale rechtlijnige vlucht met dezelfde snelheid verandert deze niet. Dan moet de totale lift dus precies aangrijpen op het zwaartepunt: dan is er immers geen totaal moment. Wordt de invalshoek iets groter, grijpt de totale lift iets achter het zwaartepunt aan en kantelt het vliegtuig weer iets met zijn neus omlaag. Wordt de invalshoek kleiner, grijpt de totale lift iets voor het zwaartepunt aan en kantelt het vliegtuig weer iets met zijn neus omhoog. Hier is het hele idee van stabiliteit op gebaseerd, en is dus de absolute basis van wat er gebeurt. Bij alle stabiele vliegtuigen gebeurt hetzelfde!
We halen er even een paar grafieken bij:



Let op: er wordt uitgegaan van een normaal assenstelsel dus alpha rechts van de y-as is positief en Cmtotal boven de x-as is ook positief.
In het eerste grafiekje is Cm total het totale Cm van het vliegtuig (het moment verandert kwadratisch met de snelheid en invalshoek, maar daar hoeven we ons geen zorgen over te maken: het Cm beeld dat uit maar is makkelijker om mee te werken omdat het een rechte lijn is. Een Cm van 0 is natuurlijk ook een moment van 0), a is alpha (invalshoek). Dit is een stabiel vliegtuig: als de invalshoek kleiner wordt, neemt de Cm toe dus kantelt het vliegtuig met zijn neus omhoog weer naar zijn originele invalshoek. Het punt waarop Cm nul is, ligt op een positieve alpha dus het vliegtuig heeft lift als het stabiel vliegt, wat erg belangrijk is!
In de tweede grafiek is het juist andersom: het vliegtuig versterkt de beweging. Het vliegtuig zal dus steeds sneller voor- of achteruit draaien als hij maar een heel klein beetje afwijkt van de invalshoek alpha op Cm=0. (Dat is een het effect wat je krijgt als je een blad papier laat vallen: het gaat tollen omdat het zwaartepunt ver achter het aerodynamisch middelpunt ligt.) Een F-16 is licht instabiel, omdat dit zorgt voor betere wendbaarheid. Door mensen zou zo'n vliegtuig niet te vliegen zijn, daarom wordt de F-16 ook eerst bestuurd door computers en dan door de piloot.
Hier tussenin zit natuurlijk ook nog een situatie: de derde grafiek. Als het vliegtuig een hogere invalshoek krijgt, blijft het gewoon met die invalshoek doorvliegen. Het is niet instabiel en niet stabiel. Ideaal dus voor een 3D kist: hij vliegt zowel op de kop als normaal met dezelfde trim. De piloot heeft hier natuurlijk wel meer werk mee en kan het vliegtuig niet voor langere tijd rechtdoor laten vliegen zonder corrigeren.
Ligt de horizontale lijn niet op de x-as maar is hij wel horizontaal, is het vliegtuig ook niet stabiel en kunnen we zien welke kant hij op zal tollen.
Nog een stapje verder: hoe een vliegtuig stabiel wordt
Nu we weten hoe een vliegtuig in zijn geheel stabiel wordt, kunnen we dit gaan toepassen op conventionele vliegtuigen. We beginnen met een begrip dat we eerder hebben gezien: het aerodynamisch middelpunt. Dat is het punt waarop het momentcoëfficiënt niet verandert en dus constant is. Bij een vleugelprofiel alleen is dit 25% van de koorde. Bij een vliegtuig speelt er meer mee, maar het principe blijft hetzelfde. Let op dat dit een coëfficiënt is en dat de totale kracht kwadratisch afhankelijk is van de vliegsnelheid en invalshoek. Het berekenen van een coëfficiënt maakt het mogelijk om een aerodynamisch middelpunt te bepalen.
Het aerodynamisch middelpunt noemen we ook wel het neutrale punt (NP). Leggen we het zwaartepunt op dit punt, draait het vliegtuig met een constante kracht om zijn as (mits de snelheid hetzelfde blijft). Dat betekent dus een constante Cm. Het middelste grafiekje boven geeft deze situatie aan: het CG ligt op het NP. De lijn kan ook hoger of lager liggen, als deze maar parallel is met de x-as weten we dat het CG op het NP ligt, en dus waar het NP ligt.
Draait het vliegtuig op dit punt met zijn neus naar beneden (negatieve Cm), kunnen we het vliegtuig helaas niet stabiel krijgen. Leggen we het zwaartepunt achter het NP, krijgen we de volgende situatie:

Het vliegtuig is hier dus helemaal instabiel.
Leggen we het zwaartepunt nu voor het NP, krijgen we de volgende situatie:

Nu zal het vliegtuig wel stabiel vliegen, maar alleen op de kop!
We weten nu dus dat het totale momentcoëfficiënt rond het NP positief moet zijn, willen we het vliegtuig stabiel kunnen laten vliegen. Dit kunnen we bereiken met het vliegtuig in het voorbeeld door het stabilo een meer negatieve hoek te geven. Als het Cm positief is met het CG op het NP, hoeven we alleen nog het CG voor het NP te leggen en krijgen we de volgende situatie:

Mooi, het vliegtuig vliegt nu stabiel. Het houdt dezelfde invalshoek en dus dezelfde snelheid. Krijgt het een iets hogere invalshoek, gaat het weer terug naar zijn oorspronkelijke invalshoek.
Nu hebben we dus bekeken dat de totale Cm positief moet zijn voor stabiliteit, dus net als een vliegende vleugel. Het totale CoP moet dus naar voren verschuiven met een lagere invalshoek.
Even een voorbeeld van een vliegende vleugel tussendoor. Het CoP verschuift naar voren bij een lagere invalshoek dus hij is stabiel, en het punt waarop het CoP gelijk is aan het CG is de invalshoek waar hij steeds naar terug keert.

Een vliegtuig moet zich dus net zo gedragen, maar dan moeten de vleugel en het staartvlak samen precies doen wat een vliegende vleugel in zijn eentje doet met een stabiel vleugelprofiel.
Nóg een stapje verder: stabiliteit bij een conventioneel vliegtuig
We weten nu wat de totale krachten op een vliegtuig doen met stabiliteit, maar nu moeten we dat nog in de praktijk brengen bij een conventioneel vliegtuig met meerdere oppervlakken. En dat is lastiger dan het lijkt.
We beginnen even met het verschil tussen invalshoek en invalshoek bij nul lift. Een normaal, gekromd vleugelprofiel heeft lift bij een invalshoek van 0. Erg belangrijk is dat die lift altijd gelijk met de invalshoek toeneemt. Nemen we dus de invalshoek bij 0 lift van twee verschillende profielen, en geven we ze dan een invalshoek die 2 graden groter is, geven ze vrijwel evenveel lift. Dat komt namelijk doordat de CL bij vrijwel alle vleugelprofielen gelijk met de invalshoek verandert, (ter informatie: met een richtingscoëfficiënt van ongeveer 2π) tot het stallpunt uiteraard. Pakken we de invalshoek bij 0 lift geven alle vleugelprofielen dus vrijwel evenveel lift bij elke invalshoek tot het stallpunt.
Daarom gebruiken we nu even de invalshoek bij 0 lift als een invalshoek van 0 graden. Dit voorkomt verwarring.
Pakken we een vliegtuig met een vleugelprofiel dat een negatief Cm heeft, en stellen we de invalshoek0lift van het staartvlak en de vleugel allebei op 0, kunnen we op onze blote voeten aanvoelen dat dit nooit stabiel te krijgen is: als er bij 0 lift en het CG op het NP een negatief moment is, is er geen stabiliteit te verkrijgen zoals we straks gezien hebben. Daarom moet de invalshoek0lift van het staartvlak altijd negatief zijn bij een profiel met een negatief Cm wil men stabiliteit verkrijgen! Dat geldt uiteraard ook voor een positief Cm van de vleugel maar dan andersom (wat echter zelden gebeurt, want dan kun je het staartvlak beter weglaten). Dit is een heel belangrijk punt en moet je goed in je achterhoofd houden.
Bij een vleugelprofiel met een negatieve Cm verschuift het CoP van dit profiel naar achteren bij een lagere invalshoek (dus hogere snelheid). Dus, om het totale CoP op het CG te houden (anders kantelt het vliegtuig naar voor of achter), moet het staartvlak steeds meer naar onderen drukken bij hogere snelheid. Inderdaad, niet andersom! Het kan dus zo zijn dat het staartvlak naar boven moet drukken bij lage snelheden en grote invalshoeken, omdat het CoP van de vleugel dan voor het CG ligt. Het vliegtuig is daarbij nog steeds even stabiel.
Belangrijk hierbij is weer het NP: het CG moet ALTIJD voor het NP liggen om stabiliteit te verkrijgen.
We halen er even de invloed van het hoogteroer bij. Het hoogteroer doet niks meer dan de gemiddelde hoek van het stabilo veranderen. We nemen even aan dat we een hoogteroer hebben dat helemaal beweegt (dus een stabilo dat van hoek verandert), dat is makkelijker werken. Als het stabilo van hoek verandert, verandert het NP vrijwel niet. Het constante Cm voor als het CG op het NP ligt verandert natuurlijk wel: kantelt het stabilo naar beneden, wordt die Cm groter: het vliegtuig wil immers liever met zijn neus naar boven kantelen dan eerder. Maar het NP verschuift dus vrijwel niet: onthoud dit even. De steilheid van de totale Cm lijn verandert dus ook niet: het vliegtuig is even stabiel. Wat wel verandert is de locatie van deze lijn: het vliegtuig is stabiel bij een hogere invalshoek (dus lagere snelheid).
Dit is een belangrijk punt: het stabilo kantelt omlaag (krijgt een meer negatieve hoek) en het vliegtuig gaat dus langzamer vliegen. Maar het stabilo gaat ook minder negatieve of meer positieve lift leveren (bij een vliegtuig met Cm<0 uiteraard) omdat het CoP van de vleugel naar voren beweegt.
Even om het goed te begrijpen: ligt het CG voor het CoP van de vleugel op dat moment, levert het stabilo negatieve lift. Ligt het CG echter achter het CoP van de vleugel op dat moment, levert het stabilo positieve lift (simpelweg hefbomen).
Stabiliteit uitgelegd in dynamische situaties
Een vliegtuig is dus in eerste instantie stabiel door het verschil in invalshoek0lift van vleugel en staartvlak. Het staartvlak kan dus ook liften. Kijk maar naar canards: daar is de canard in principe een kleine vleugel en de hoofdvleugel een groot stabilo. De canard moet ook een grotere invalshoek0lift hebben dan de hoofdvleugel: hetzelfde als een vleugel en stabilo.
Let even op: Als een vliegtuig in de praktijk door een verstoring een iets lagere invalshoek krijgt, duurt het heel even voordat het vliegtuig zich weer hersteld heeft naar de invalshoek waarbij hij stabiliteit heeft. Dit nemen we echter niet mee omdat dit niet van belang is voor het begrip stabiliteit, en voor de rest er ook niet echt toe doet (behalve als je pitch oscillaties gaat bestuderen...).
Het stabilo van een vliegtuig kan dus naar onder of naar boven drukken, afhankelijk van de vliegsituatie. Je hebt nu ook gezien dat bij 0 lift en een vleugel met Cm<0 het stabilo altijd omlaag moet drukken om het negatieve moment tegen te gaan. Het aerodynamisch middelpunt (NP) van een vleugelprofiel ligt rond 25% koorde, maar bij een vliegtuig helpt de staart ook nog mee dus ligt het aerodynamisch middelpunt van het totale vliegtuig verder naar achteren. Is de invalhoek groot (dus de snelheid laag) dicteert de formule voor momentcoëfficiënt dat het CoP vrij dicht bij die 25% op de vleugel moet liggen. Het zwaartepunt kan hier achter liggen, en in zo'n situatie levert het stabilo dus lift!
Ligt het CoP van de vleugel al op het CG, hoeft het stabilo niks meer te doen en levert hij dus 0 lift.
>Nog even een voorbeeld: nemen we een vliegtuig met een symmetrisch profiel, is het Cm nul en verandert de positie van het CoP op het vleugelprofiel dus niet. Het NP ligt achter het CoP van het vleugelprofiel, dankzij het stabilo. Het CG ligt voor het NP. Afhankelijk van of het CG voor of achter het CoP van de vleugel ligt, levert het stabilo altijd positieve of negatieve lift. Ligt het CG precies op het CoP van de vleugel (ongeveer 25% dus), levert het stabilo altijd 0 lift. Maar hij zorgt daarbij natuurlijk wel voor stabiliteit: komt er een verstoring, levert het stabilo positieve of negatieve lift zodat de situatie weer terugkeert naar de stabiele invalshoek.
Samengevat: het hoogteroer in de praktijk
Als je dus aan het vliegen bent en je geeft hoogteroer omhoog of omlaag, verander je dus het punt van stabiliteit. Met een bepaalde hoogteroeruitslag is het vliegtuig stabiel op een bepaalde invalshoek. Geef je echter teveel hoogteroeruitslag, is je vliegtuig nog wel stabiel maar kan hij stabiel zijn over het stallpunt, dus je vliegtuig overtrekt. Geef je teveel negatieve hoogteroeruitslag, kan het vliegtuig stabiel zijn op de kop.
Geef je wat 'up' als je gewoon rechtdoor vliegt, is je vliegtuig nog steeds stabiel maar krijgt hij een hogere invalshoek. Hij krijgt dus meer lift dan gewicht. Zo kun je een bocht door vliegen. Vlieg je echter steeds meer omhoog, zal je vliegtuig meer en meer snelheid verliezen. Hij zal nog steeds stabiel zijn op die ene invalshoek maar dus minder lift dan gewicht produceren en met zijn neus omlaag kantelen. Als hij omlaag vliegt zal hij weer iets sneller gaan vliegen (door de omzetting van potentiële in kinetische energie) en dus meer lift gaan produceren dan gewicht. De invalshoek blijft dus de hele tijd hetzelfde omdat hij op dat punt stabiel is! Het vliegtuig zal een sinusoïde gaan beschrijven. Daarom is een té stabiel vliegtuig ook niet goed: deze zal al snel gaan 'dolfijnen'.
Extra: Stabiliteit beoordelen
Om de stabiliteit van een vliegtuig te beoordelen zijn er een paar concepten. De eerste is Static Margin. Dat is eigenlijk heel simpel: het is het procent in koorde dat het CG voor het NP ligt. Heb je een vleugel met koorde 20cm, NP op 9cm en het CG op 7cm heb je een SM van: (9-7)/20*100=10%. Een SM ligt meestal zo tussen de 5% en 15%, maar kan uiteraard ook lager of hoger zijn. Hoger is erg stabiel, lager is minder stabiel. Een negatieve SM betekent dat het vliegtuig onstabiel is. Wat de SM niet meeneemt is dat een vliegtuig met een SM van 10% wel stabiel kan zijn, maar dat de stabiele invalshoek boven het stallpunt ligt door de hoge positieve totale Cm. Je moet dan dus vliegen met veel down of je stabilo een meer positieve (of minder negatieve) invalshoek geven.
Noemenswaardig is ook het MAC: heb je geen rechte vleugel, gebruik je het Mean Aerodynamic Chord, kortweg MAC. Dit is de gemiddelde aerodynamische koorde.
Om de stabiliteit uit te drukken hebben we het begrip Static Margin, maar die geeft niet weer of de staart groot genoeg is om de krachten van de vleugel op te vangen. Dat drukken we uit in Tail Volume. Deze heb je zowel voor het horizontale staartvlak als het verticale staartvlak. De formules:
W=wing, H=horizontal, V=vertical, A=area, C=chord, S=span, M=moment (afstand van het NP van de vleugel tot het NP van de staart, 25%-25% dus)
Verticale staartvlak volume = ((VA*VM)/(WA*WS))
Horizontale staartvlak volume = ((HA*HM)/(WA*WC))
Deze kunnen verschillende waardes hebben. Ik ga me niet wagen aan het geven van richtwaardes, deze zijn wel te vinden.
Extra: Stabiliteit berekenen
Stabiliteit kun je met software uitrekenen. De makkelijkste software daarvoor is XFLR5, en ook nog gratis. Het maakt gebruik van 2D analyses van vleugelprofielen met XFOIL, en berekent die daarna door naar 3D met de Lifting Line theorie of andere methodes. Daarnaast is het niet moeilijk te leren.
De laatste tijd heb ik ontzettend veel geleerd over stabiliteit. Je voorstellen hoe een vliegtuig zich gedraagt in dynamische situaties is moeilijk, maar het scheelt als je alle concepten goed snapt en nergens mee in de war komt. Uiteindelijk snap je dan hoe een vliegtuig stabiel kan vliegen. Ik hoop dat dit stuk tekst meer mensen de mogelijkheid geeft om zich hierin te verdiepen. Want, als je het eenmaal snapt, is het best leuk.
De eerste afbeelding is gemaakt met JavaFoil, de afbeeldingen met vleugelprofielen zijn gemaakt met XFLR5 en photoshop, de rest is helemaal gemaakt in photoshop. Alle afbeeldingen mogen vrij gebruikt worden. Een presentatie waarvan ik veel ideeën heb gekregen:
http://xflr5.sourceforge.net/docs/XFLR5_and_Stability_analysis.pdf
Dit deel gaat over stabiliteit. In andere woorden, wat het verschil is tussen een blaadje papier en jouw vliegtuig. Ik heb geprobeerd het zo overzichtelijk mogelijk te houden en alles zo duidelijk mogelijk uit te leggen. De terminologie heb ik ook zo simpel mogelijk gehouden. Alle tips ter verbetering zijn natuurlijk welkom, bijvoorbeeld qua duidelijkheid. Ik krijg er een punt voor dus misschien help je me wel aan een hoger punt.
De afbeeldingen zijn in het Engels aangezien ik van plan ben dit ook daarin te vertalen. Schrik niet van die paar formules, er zit zo weinig mogelijk wiskunde in.
[size=+2]Stabiliteit[/size]
De basis
Een vleugelprofiel genereert lift door de lucht af te buigen. De over- of onderdruk rond een vleugelprofiel trekt en duwt als het ware aan het profiel, loodrecht op het stukje waar de betreffende druk op duwt. Alle kleine stukjes trek- en duwkracht bij elkaar opgeteld zorgen ervoor dat een profiel een liftkracht opwekt. In de volgende afbeelding zijn de drukvectoren weergegeven: rood is een harde drukkracht, blauw andersom. Het profiel levert in deze situatie lift.

Maar stel nu dat de lift nul is: er is geen liftkracht. Dan zorgen alle trek- en duwkrachten ervoor dat het profiel toch nog een beetje om zijn as wil draaien. Dit noemen we het moment. Een symmetrisch profiel heeft bij nul lift geen moment: de krachten zijn immers overal in spiegelbeeld en zorgen er dus niet voor dat het profiel nog een kant op wil draaien.
Gaat het profiel nu lift leveren, zorgen alle trek- en duwkrachten voor een totale liftkracht. Deze kun je overal op het profiel meten, maar dan krijg je én een liftkracht én een momentkracht (hij draait om zijn as). Hier hebben we natuurlijk niks aan, daarom hebben we het 'Center of Pressure' (van nu af aan CoP) bedacht. Dit is het punt op het profiel waar bij een bepaalde invalshoek de lift aangrijpt, zonder momentkracht. Als je het profiel op dit punt bij een bepaalde invalhoek vast houdt, voel je dus alleen een kracht omhoog en geen draaikracht.
Dit punt blijft niet hetzelfde met invalshoek: het verschuift. Bij nul lift is er geen liftkracht, dus als het profiel met zijn neus omlaag wil kantelen ligt het CoP oneindig ver achter het profiel en is hij ook oneindig klein: er is immers geen lift.
Om profielen te kunnen vergelijken is er de 'Momentcoëfficiënt' (vanaf nu Cm). De formule daarvoor is:
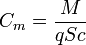
M is daarbij de momentkracht, S het vleugeloppervlak, c de koorde en q de dynamische druk. Het vleugeloppervlak en de koorde blijven bij een vliegtuig natuurlijk constant, deze kunnen we even weglaten. De dynamische druk q is nauw verwant met de kinetische energie van een deeltje (je weet wel, ½mv2) en dit is de formule ervoor:
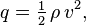
Waarbij p (rho) de luchtdichtheid is (op zeeniveau 1,23) en v de snelheid.
We meten de momentcoëfficiënt altijd op 25% van de koorde. Het feit wil namelijk dat het momentcoëfficiënt nauwelijks verandert rond dit punt (het is het aerodynamisch middelpunt van het profiel). Dit is vooral zo bij dunne symmetrische profielen, het Cm fluctueert steeds meer naarmate het profiel dikker en minder symmetrisch wordt. We nemen even aan dat Cm constant is, hoewel hij in de praktijk toch iets verschuift met invalshoek, maar niet veel.
Als we de tweede formule bij de Cm formule leggen en stellen dat Cm constant is, zien we dat het totale moment kwadratisch toeneemt met de snelheid. De snelheid hangt samen met de invalshoek: hoe lager de invalshoek, hoe groter de snelheid. De lift blijft gelijk, dus de plek van het CoP moet verschuiven: anders kan er geen verandering in moment komen. We kunnen dus afleiden dat als het Cm negatief is, het moment ook altijd negatief is. Let op: we hebben afgesproken dat het moment (en dus Cm) negatief is als het profiel met zijn neus omlaag wil kantelen!
We weten nu dus dat met een negatief Cm het CoP naar achteren verschuift met hogere snelheid, dus lagere invalshoek.
We hebben 3 soorten profielen: die waarbij het Cm negatief is, die waarbij het Cm 0 is en die waarbij het Cm positief is. Symmetrische profielen hebben altijd een Cm van 0, maar we hebben ook profielen die niet symmetrisch zijn met een Cm van 0. We gaan nu eerst bekijken wat er bij deze verschillende soorten profielen met het CoP gebeurt met AOA (AOA = Angle Of Attack, invalshoek):

De pijl die de plaats van het CoP aangeeft is net zo groot als de liftcoëfficiënt. Is de pijl dus 4 keer zo klein, kun je 2 keer zo snel vliegen. De snelheid varieert en die pijl blijft dus bij een vliegtuig altijd even groot. Hij verschuift dus wel en verandert daarmee het punt waarop de lift van de vleugel aangrijpt.
Een stapje verder: hoe stabiliteit werkt
Als een vliegtuig een bepaalde invalshoek (dus snelheid) heeft, willen we dat het vliegtuig deze snelheid houdt. Krijgt het vliegtuig een iets andere invalshoek, willen we dat het vliegtuig zichzelf corrigeert en weer zijn oorspronkelijke invalshoek aanneemt.
Dat kunnen we op verschillende manieren realiseren, maar we bekijken het vliegtuig even als een geheel. Het heeft een bepaalde invalshoek, en in normale rechtlijnige vlucht met dezelfde snelheid verandert deze niet. Dan moet de totale lift dus precies aangrijpen op het zwaartepunt: dan is er immers geen totaal moment. Wordt de invalshoek iets groter, grijpt de totale lift iets achter het zwaartepunt aan en kantelt het vliegtuig weer iets met zijn neus omlaag. Wordt de invalshoek kleiner, grijpt de totale lift iets voor het zwaartepunt aan en kantelt het vliegtuig weer iets met zijn neus omhoog. Hier is het hele idee van stabiliteit op gebaseerd, en is dus de absolute basis van wat er gebeurt. Bij alle stabiele vliegtuigen gebeurt hetzelfde!
We halen er even een paar grafieken bij:



Let op: er wordt uitgegaan van een normaal assenstelsel dus alpha rechts van de y-as is positief en Cmtotal boven de x-as is ook positief.
In het eerste grafiekje is Cm total het totale Cm van het vliegtuig (het moment verandert kwadratisch met de snelheid en invalshoek, maar daar hoeven we ons geen zorgen over te maken: het Cm beeld dat uit maar is makkelijker om mee te werken omdat het een rechte lijn is. Een Cm van 0 is natuurlijk ook een moment van 0), a is alpha (invalshoek). Dit is een stabiel vliegtuig: als de invalshoek kleiner wordt, neemt de Cm toe dus kantelt het vliegtuig met zijn neus omhoog weer naar zijn originele invalshoek. Het punt waarop Cm nul is, ligt op een positieve alpha dus het vliegtuig heeft lift als het stabiel vliegt, wat erg belangrijk is!
In de tweede grafiek is het juist andersom: het vliegtuig versterkt de beweging. Het vliegtuig zal dus steeds sneller voor- of achteruit draaien als hij maar een heel klein beetje afwijkt van de invalshoek alpha op Cm=0. (Dat is een het effect wat je krijgt als je een blad papier laat vallen: het gaat tollen omdat het zwaartepunt ver achter het aerodynamisch middelpunt ligt.) Een F-16 is licht instabiel, omdat dit zorgt voor betere wendbaarheid. Door mensen zou zo'n vliegtuig niet te vliegen zijn, daarom wordt de F-16 ook eerst bestuurd door computers en dan door de piloot.
Hier tussenin zit natuurlijk ook nog een situatie: de derde grafiek. Als het vliegtuig een hogere invalshoek krijgt, blijft het gewoon met die invalshoek doorvliegen. Het is niet instabiel en niet stabiel. Ideaal dus voor een 3D kist: hij vliegt zowel op de kop als normaal met dezelfde trim. De piloot heeft hier natuurlijk wel meer werk mee en kan het vliegtuig niet voor langere tijd rechtdoor laten vliegen zonder corrigeren.
Ligt de horizontale lijn niet op de x-as maar is hij wel horizontaal, is het vliegtuig ook niet stabiel en kunnen we zien welke kant hij op zal tollen.
Nog een stapje verder: hoe een vliegtuig stabiel wordt
Nu we weten hoe een vliegtuig in zijn geheel stabiel wordt, kunnen we dit gaan toepassen op conventionele vliegtuigen. We beginnen met een begrip dat we eerder hebben gezien: het aerodynamisch middelpunt. Dat is het punt waarop het momentcoëfficiënt niet verandert en dus constant is. Bij een vleugelprofiel alleen is dit 25% van de koorde. Bij een vliegtuig speelt er meer mee, maar het principe blijft hetzelfde. Let op dat dit een coëfficiënt is en dat de totale kracht kwadratisch afhankelijk is van de vliegsnelheid en invalshoek. Het berekenen van een coëfficiënt maakt het mogelijk om een aerodynamisch middelpunt te bepalen.
Het aerodynamisch middelpunt noemen we ook wel het neutrale punt (NP). Leggen we het zwaartepunt op dit punt, draait het vliegtuig met een constante kracht om zijn as (mits de snelheid hetzelfde blijft). Dat betekent dus een constante Cm. Het middelste grafiekje boven geeft deze situatie aan: het CG ligt op het NP. De lijn kan ook hoger of lager liggen, als deze maar parallel is met de x-as weten we dat het CG op het NP ligt, en dus waar het NP ligt.
Draait het vliegtuig op dit punt met zijn neus naar beneden (negatieve Cm), kunnen we het vliegtuig helaas niet stabiel krijgen. Leggen we het zwaartepunt achter het NP, krijgen we de volgende situatie:

Het vliegtuig is hier dus helemaal instabiel.
Leggen we het zwaartepunt nu voor het NP, krijgen we de volgende situatie:

Nu zal het vliegtuig wel stabiel vliegen, maar alleen op de kop!
We weten nu dus dat het totale momentcoëfficiënt rond het NP positief moet zijn, willen we het vliegtuig stabiel kunnen laten vliegen. Dit kunnen we bereiken met het vliegtuig in het voorbeeld door het stabilo een meer negatieve hoek te geven. Als het Cm positief is met het CG op het NP, hoeven we alleen nog het CG voor het NP te leggen en krijgen we de volgende situatie:

Mooi, het vliegtuig vliegt nu stabiel. Het houdt dezelfde invalshoek en dus dezelfde snelheid. Krijgt het een iets hogere invalshoek, gaat het weer terug naar zijn oorspronkelijke invalshoek.
Nu hebben we dus bekeken dat de totale Cm positief moet zijn voor stabiliteit, dus net als een vliegende vleugel. Het totale CoP moet dus naar voren verschuiven met een lagere invalshoek.
Even een voorbeeld van een vliegende vleugel tussendoor. Het CoP verschuift naar voren bij een lagere invalshoek dus hij is stabiel, en het punt waarop het CoP gelijk is aan het CG is de invalshoek waar hij steeds naar terug keert.

Een vliegtuig moet zich dus net zo gedragen, maar dan moeten de vleugel en het staartvlak samen precies doen wat een vliegende vleugel in zijn eentje doet met een stabiel vleugelprofiel.
Nóg een stapje verder: stabiliteit bij een conventioneel vliegtuig
We weten nu wat de totale krachten op een vliegtuig doen met stabiliteit, maar nu moeten we dat nog in de praktijk brengen bij een conventioneel vliegtuig met meerdere oppervlakken. En dat is lastiger dan het lijkt.
We beginnen even met het verschil tussen invalshoek en invalshoek bij nul lift. Een normaal, gekromd vleugelprofiel heeft lift bij een invalshoek van 0. Erg belangrijk is dat die lift altijd gelijk met de invalshoek toeneemt. Nemen we dus de invalshoek bij 0 lift van twee verschillende profielen, en geven we ze dan een invalshoek die 2 graden groter is, geven ze vrijwel evenveel lift. Dat komt namelijk doordat de CL bij vrijwel alle vleugelprofielen gelijk met de invalshoek verandert, (ter informatie: met een richtingscoëfficiënt van ongeveer 2π) tot het stallpunt uiteraard. Pakken we de invalshoek bij 0 lift geven alle vleugelprofielen dus vrijwel evenveel lift bij elke invalshoek tot het stallpunt.
Daarom gebruiken we nu even de invalshoek bij 0 lift als een invalshoek van 0 graden. Dit voorkomt verwarring.
Pakken we een vliegtuig met een vleugelprofiel dat een negatief Cm heeft, en stellen we de invalshoek0lift van het staartvlak en de vleugel allebei op 0, kunnen we op onze blote voeten aanvoelen dat dit nooit stabiel te krijgen is: als er bij 0 lift en het CG op het NP een negatief moment is, is er geen stabiliteit te verkrijgen zoals we straks gezien hebben. Daarom moet de invalshoek0lift van het staartvlak altijd negatief zijn bij een profiel met een negatief Cm wil men stabiliteit verkrijgen! Dat geldt uiteraard ook voor een positief Cm van de vleugel maar dan andersom (wat echter zelden gebeurt, want dan kun je het staartvlak beter weglaten). Dit is een heel belangrijk punt en moet je goed in je achterhoofd houden.
Bij een vleugelprofiel met een negatieve Cm verschuift het CoP van dit profiel naar achteren bij een lagere invalshoek (dus hogere snelheid). Dus, om het totale CoP op het CG te houden (anders kantelt het vliegtuig naar voor of achter), moet het staartvlak steeds meer naar onderen drukken bij hogere snelheid. Inderdaad, niet andersom! Het kan dus zo zijn dat het staartvlak naar boven moet drukken bij lage snelheden en grote invalshoeken, omdat het CoP van de vleugel dan voor het CG ligt. Het vliegtuig is daarbij nog steeds even stabiel.
Belangrijk hierbij is weer het NP: het CG moet ALTIJD voor het NP liggen om stabiliteit te verkrijgen.
We halen er even de invloed van het hoogteroer bij. Het hoogteroer doet niks meer dan de gemiddelde hoek van het stabilo veranderen. We nemen even aan dat we een hoogteroer hebben dat helemaal beweegt (dus een stabilo dat van hoek verandert), dat is makkelijker werken. Als het stabilo van hoek verandert, verandert het NP vrijwel niet. Het constante Cm voor als het CG op het NP ligt verandert natuurlijk wel: kantelt het stabilo naar beneden, wordt die Cm groter: het vliegtuig wil immers liever met zijn neus naar boven kantelen dan eerder. Maar het NP verschuift dus vrijwel niet: onthoud dit even. De steilheid van de totale Cm lijn verandert dus ook niet: het vliegtuig is even stabiel. Wat wel verandert is de locatie van deze lijn: het vliegtuig is stabiel bij een hogere invalshoek (dus lagere snelheid).
Dit is een belangrijk punt: het stabilo kantelt omlaag (krijgt een meer negatieve hoek) en het vliegtuig gaat dus langzamer vliegen. Maar het stabilo gaat ook minder negatieve of meer positieve lift leveren (bij een vliegtuig met Cm<0 uiteraard) omdat het CoP van de vleugel naar voren beweegt.
Even om het goed te begrijpen: ligt het CG voor het CoP van de vleugel op dat moment, levert het stabilo negatieve lift. Ligt het CG echter achter het CoP van de vleugel op dat moment, levert het stabilo positieve lift (simpelweg hefbomen).
Stabiliteit uitgelegd in dynamische situaties
Een vliegtuig is dus in eerste instantie stabiel door het verschil in invalshoek0lift van vleugel en staartvlak. Het staartvlak kan dus ook liften. Kijk maar naar canards: daar is de canard in principe een kleine vleugel en de hoofdvleugel een groot stabilo. De canard moet ook een grotere invalshoek0lift hebben dan de hoofdvleugel: hetzelfde als een vleugel en stabilo.
Let even op: Als een vliegtuig in de praktijk door een verstoring een iets lagere invalshoek krijgt, duurt het heel even voordat het vliegtuig zich weer hersteld heeft naar de invalshoek waarbij hij stabiliteit heeft. Dit nemen we echter niet mee omdat dit niet van belang is voor het begrip stabiliteit, en voor de rest er ook niet echt toe doet (behalve als je pitch oscillaties gaat bestuderen...).
Het stabilo van een vliegtuig kan dus naar onder of naar boven drukken, afhankelijk van de vliegsituatie. Je hebt nu ook gezien dat bij 0 lift en een vleugel met Cm<0 het stabilo altijd omlaag moet drukken om het negatieve moment tegen te gaan. Het aerodynamisch middelpunt (NP) van een vleugelprofiel ligt rond 25% koorde, maar bij een vliegtuig helpt de staart ook nog mee dus ligt het aerodynamisch middelpunt van het totale vliegtuig verder naar achteren. Is de invalhoek groot (dus de snelheid laag) dicteert de formule voor momentcoëfficiënt dat het CoP vrij dicht bij die 25% op de vleugel moet liggen. Het zwaartepunt kan hier achter liggen, en in zo'n situatie levert het stabilo dus lift!
Ligt het CoP van de vleugel al op het CG, hoeft het stabilo niks meer te doen en levert hij dus 0 lift.
>Nog even een voorbeeld: nemen we een vliegtuig met een symmetrisch profiel, is het Cm nul en verandert de positie van het CoP op het vleugelprofiel dus niet. Het NP ligt achter het CoP van het vleugelprofiel, dankzij het stabilo. Het CG ligt voor het NP. Afhankelijk van of het CG voor of achter het CoP van de vleugel ligt, levert het stabilo altijd positieve of negatieve lift. Ligt het CG precies op het CoP van de vleugel (ongeveer 25% dus), levert het stabilo altijd 0 lift. Maar hij zorgt daarbij natuurlijk wel voor stabiliteit: komt er een verstoring, levert het stabilo positieve of negatieve lift zodat de situatie weer terugkeert naar de stabiele invalshoek.
Samengevat: het hoogteroer in de praktijk
Als je dus aan het vliegen bent en je geeft hoogteroer omhoog of omlaag, verander je dus het punt van stabiliteit. Met een bepaalde hoogteroeruitslag is het vliegtuig stabiel op een bepaalde invalshoek. Geef je echter teveel hoogteroeruitslag, is je vliegtuig nog wel stabiel maar kan hij stabiel zijn over het stallpunt, dus je vliegtuig overtrekt. Geef je teveel negatieve hoogteroeruitslag, kan het vliegtuig stabiel zijn op de kop.
Geef je wat 'up' als je gewoon rechtdoor vliegt, is je vliegtuig nog steeds stabiel maar krijgt hij een hogere invalshoek. Hij krijgt dus meer lift dan gewicht. Zo kun je een bocht door vliegen. Vlieg je echter steeds meer omhoog, zal je vliegtuig meer en meer snelheid verliezen. Hij zal nog steeds stabiel zijn op die ene invalshoek maar dus minder lift dan gewicht produceren en met zijn neus omlaag kantelen. Als hij omlaag vliegt zal hij weer iets sneller gaan vliegen (door de omzetting van potentiële in kinetische energie) en dus meer lift gaan produceren dan gewicht. De invalshoek blijft dus de hele tijd hetzelfde omdat hij op dat punt stabiel is! Het vliegtuig zal een sinusoïde gaan beschrijven. Daarom is een té stabiel vliegtuig ook niet goed: deze zal al snel gaan 'dolfijnen'.
Extra: Stabiliteit beoordelen
Om de stabiliteit van een vliegtuig te beoordelen zijn er een paar concepten. De eerste is Static Margin. Dat is eigenlijk heel simpel: het is het procent in koorde dat het CG voor het NP ligt. Heb je een vleugel met koorde 20cm, NP op 9cm en het CG op 7cm heb je een SM van: (9-7)/20*100=10%. Een SM ligt meestal zo tussen de 5% en 15%, maar kan uiteraard ook lager of hoger zijn. Hoger is erg stabiel, lager is minder stabiel. Een negatieve SM betekent dat het vliegtuig onstabiel is. Wat de SM niet meeneemt is dat een vliegtuig met een SM van 10% wel stabiel kan zijn, maar dat de stabiele invalshoek boven het stallpunt ligt door de hoge positieve totale Cm. Je moet dan dus vliegen met veel down of je stabilo een meer positieve (of minder negatieve) invalshoek geven.
Noemenswaardig is ook het MAC: heb je geen rechte vleugel, gebruik je het Mean Aerodynamic Chord, kortweg MAC. Dit is de gemiddelde aerodynamische koorde.
Om de stabiliteit uit te drukken hebben we het begrip Static Margin, maar die geeft niet weer of de staart groot genoeg is om de krachten van de vleugel op te vangen. Dat drukken we uit in Tail Volume. Deze heb je zowel voor het horizontale staartvlak als het verticale staartvlak. De formules:
W=wing, H=horizontal, V=vertical, A=area, C=chord, S=span, M=moment (afstand van het NP van de vleugel tot het NP van de staart, 25%-25% dus)
Verticale staartvlak volume = ((VA*VM)/(WA*WS))
Horizontale staartvlak volume = ((HA*HM)/(WA*WC))
Deze kunnen verschillende waardes hebben. Ik ga me niet wagen aan het geven van richtwaardes, deze zijn wel te vinden.
Extra: Stabiliteit berekenen
Stabiliteit kun je met software uitrekenen. De makkelijkste software daarvoor is XFLR5, en ook nog gratis. Het maakt gebruik van 2D analyses van vleugelprofielen met XFOIL, en berekent die daarna door naar 3D met de Lifting Line theorie of andere methodes. Daarnaast is het niet moeilijk te leren.
De laatste tijd heb ik ontzettend veel geleerd over stabiliteit. Je voorstellen hoe een vliegtuig zich gedraagt in dynamische situaties is moeilijk, maar het scheelt als je alle concepten goed snapt en nergens mee in de war komt. Uiteindelijk snap je dan hoe een vliegtuig stabiel kan vliegen. Ik hoop dat dit stuk tekst meer mensen de mogelijkheid geeft om zich hierin te verdiepen. Want, als je het eenmaal snapt, is het best leuk.
De eerste afbeelding is gemaakt met JavaFoil, de afbeeldingen met vleugelprofielen zijn gemaakt met XFLR5 en photoshop, de rest is helemaal gemaakt in photoshop. Alle afbeeldingen mogen vrij gebruikt worden. Een presentatie waarvan ik veel ideeën heb gekregen:
http://xflr5.sourceforge.net/docs/XFLR5_and_Stability_analysis.pdf
Laatst bewerkt:









