Fotor
Forum veteraan
Ik wil graag de snelheidspolaire van een zweefvliegtuig uitleggen. Hier zijn enkele zeer interessante zaken uit te halen die het begrip van zweefvliegen kunnen verbeteren. Vooral de vraag: 'Hoe snel kan ik het beste vliegen?'.
Ik begin met de basis, de polaire van een zweefvliegtuig dat vliegt in stille lucht (geen wind, geen vertikale bewegingen).
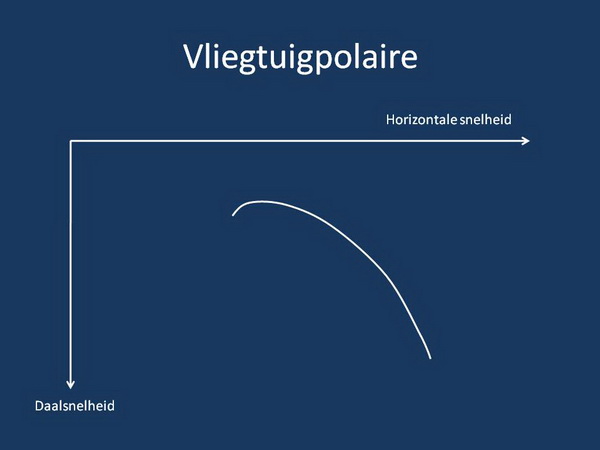
Deze figuur laat zien wat de daalsnelheid van het vliegtuig (vertikale as) is bij een gegeven vliegsnelheid (horizontale as). Voor alle duidelijkheid: voor elk zweefvliegtuig is de vorm van deze polaire anders! Deze polaire geldt voor één bepaald fictief type zwever. Exacte getallen zijn even niet belangrijk.
In deze figuur zijn een aantal plaatsen interessant.
Allereerst het meest linkse punt van de polaire. Deze geeft de minimum vliegsnelheid aan. Langzamer kan het vliegtuig niet vliegen, dan laat de stroming los van de vleugel. Links van dit punt bestaat de polaire dus simpelweg niet.
Dan het bovenste punt van de polaire.
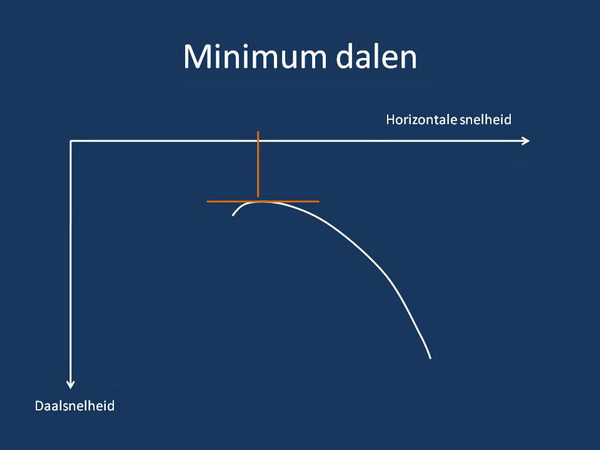
Dit punt geeft de minimale daalsnelheid weer van het model. De snelheid bij de rode vertikale lijn is dus de vliegsnelheid waarbij het model zo langzaam mogelijk naar beneden komt. Deze snelheid is interessant in een thermiekbel (bij minimaal eigen daalsnelheid ga je het hardst omhoog) of op stille dagen (dan blijf je zo lang mogelijk in de lucht).
De lijn vanuit de oorsprong die de polaire raakt

Dit punt in de polaire geeft aan bij welke snelheid het vliegtuig de beste glijhoek heeft. De verhouding horizontale snelheid/vertikale snelheid is hier optimaal. De glijhoek is simpelweg de verhouding tussen deze 2. Een glijhoek van 1:20 betekent dat je met 1 meter hoogteverlies 20 meter afstand af kunt leggen. Voor elk ander punt in de polaire is de verhouding horizontale/vertikale snelheid slechter.
Deze snelheid is interessant als je zoveel mogelijk lucht wilt doorkruisen, bijvoorbeeld tijdens het zoeken naar een bel. Als je vliegtuig deze snelheid vliegt kan hij met een gegeven hoogte zoveel mogelijk meters afleggen.
De snelheid voor beste glijhoek ligt meestal zo'n 20-30% hoger dan de snelheid voor minimum dalen. De daalsnelheid ligt echter veel minder dan 20-30% hoger, vandaar de toename in glijhoek. Bij deze snelheid gaat je zwever 'lopen'.
Als je nog sneller gaat vliegen blijft de glijhoek vaak redelijk op peil tot een gegeven snelheid, waarbij je een soort knik in de polaire ziet. In deze figuur zit een lichte knik, hoe erg de knik is hangt van het vliegtuig af. Bij oude zwevers is de knik veel erger (en bij een lagere snelheid) aanwezig dan bij moderne zwevers. Boven de snelheid waar die knik zit wordt het vliegtuig ineens minder efficient en wordt de glijhoek ineens rap slechter bij toenemende snelheid. Het is zaak beneden de vliegsnelheid van deze knik te blijven.
Nu gaan we eens kijken wat de invloed van wind is.
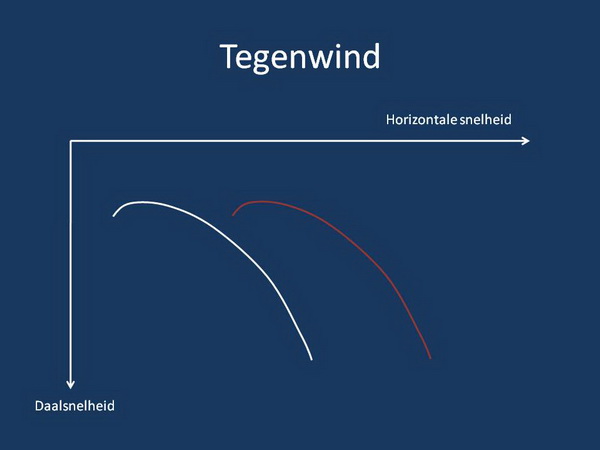
De rode polaire is de basis polaire zoals hierboven getekend, dus in stille lucht. Als we nu tegen wind in moeten gaan vliegen is de grondsnelheid lager dan de vliegsnelheid. De witte lijn is de polaire tov de grond als je tegen wind in vliegt. Hoe meer wind, hoe meer de polaire opschuift.
Nu wil ik weten wat de invloed van die wind is op de glijhoek tov de grond.
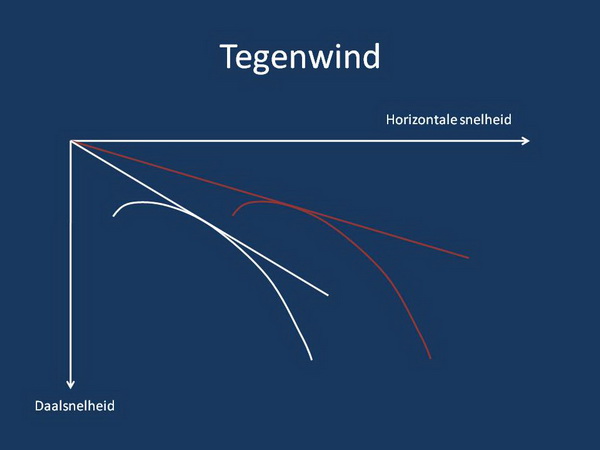
Uit deze figuur zijn 2 belangrijke conclusies te trekken.
1) De glijhoek tov de grond in tegenwind is slechter dan zonder wind.
2) De vliegsnelheid waarbij de beste glijhoek tov de grond wordt gehaald is hoger dan zonder wind. De raaklijn ligt nl op een punt verder langs de kromme, dus bij een hogere vliegsnelheid.
Stel je nu het volgende voor: je bent in een matige bel geklommen, en ondertussen is je vliegtuig door de wind benedenwinds geraakt. Nu wil je naar jezelf terugvliegen. Dat wil je doen met de beste glijhoek tov de grond. Veel mensen hebben de natuurlijke neiging de neus omhoog te trekken, omdat ze het vliegtuig anders zo hard zien zakken. Dat is nu net niet goed! Als je langzamer gaat vliegen neemt de glijhoek tov de grond drastisch af. Je moet juist wat sneller gaan vliegen. Ja, je vliegtuig zakt dan wat harder, maar hij gaat ineens ook veel beter vooruit komen, waardoor je toch beter terugkomt.
Bij meewind schuift de polaire de andere kant op. Het effect is dan dat de vliegsnelheid voor beste glijhoek wat afneemt, maar het verschil is veel kleiner dan bij tegenwind. Bij meewind voldoet in de praktijk de snelheid voor minimum daalsnelheid goed.
De invloed van stijgende / dalende lucht.
Stel nu dat je door een stuk lucht vliegt dat daalt.
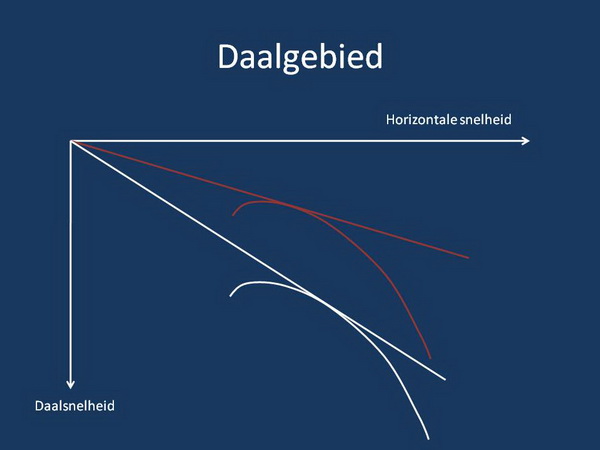
De rode lijn is weer de oorspronkelijke polaire, de witte is de polaire in de dalende lucht. We zien nu dat de beste glijhoek tov de grond in dalende lucht bij een hogere vliegsnelheid ligt dan in stille lucht. Dat betekent dat je ook in dalende lucht beter wat harder kunt gaan vliegen. Ook hier voelt het onnatuurlijk aan omdat je door harder te gaan vliegen de daalsnelheid verder toe laat nemen, en die is al zo hoog in de dalende lucht. Maar toch kom je wel beter vooruit waardoor je eerder door het daalgebied heen bent.
Bij stijgende lucht schuift de polaire de andere kant op:
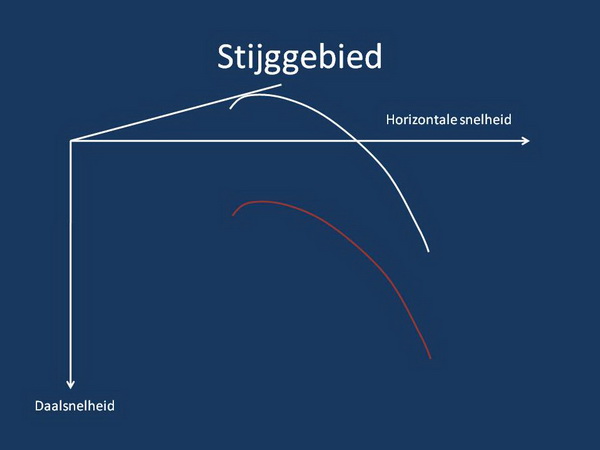
Ik heb hier de raaklijn vanuit de oorsprong aan de polaire ingetekend, maar eigenlijk is de snelheid die hierbij hoort niet interessant. Deze geeft nl de beste stijghoek tov de grond. Maar in een bel ga je draaien en is de stijghoek niet belangrijk. Het is belangrijker dat je zo snel mogelijk omhoog komt. En dat doe je met de snelheid waarbij de eigen daalsnelheid van het vliegtuig minimaal is. Als je langzamer gaat vliegen dan deze snelheid zit je bovendien erg dicht bij de overtrek. De invalshoek tijdens vliegen in thermiek verandert nogal door turbulentie in de bel, dus je wilt niet te langzaam vliegen, anders heb je de helft van de tijd loslatende stroming op je vleugel. Weg efficientie....
Ik begin met de basis, de polaire van een zweefvliegtuig dat vliegt in stille lucht (geen wind, geen vertikale bewegingen).

Deze figuur laat zien wat de daalsnelheid van het vliegtuig (vertikale as) is bij een gegeven vliegsnelheid (horizontale as). Voor alle duidelijkheid: voor elk zweefvliegtuig is de vorm van deze polaire anders! Deze polaire geldt voor één bepaald fictief type zwever. Exacte getallen zijn even niet belangrijk.
In deze figuur zijn een aantal plaatsen interessant.
Allereerst het meest linkse punt van de polaire. Deze geeft de minimum vliegsnelheid aan. Langzamer kan het vliegtuig niet vliegen, dan laat de stroming los van de vleugel. Links van dit punt bestaat de polaire dus simpelweg niet.
Dan het bovenste punt van de polaire.

Dit punt geeft de minimale daalsnelheid weer van het model. De snelheid bij de rode vertikale lijn is dus de vliegsnelheid waarbij het model zo langzaam mogelijk naar beneden komt. Deze snelheid is interessant in een thermiekbel (bij minimaal eigen daalsnelheid ga je het hardst omhoog) of op stille dagen (dan blijf je zo lang mogelijk in de lucht).
De lijn vanuit de oorsprong die de polaire raakt

Dit punt in de polaire geeft aan bij welke snelheid het vliegtuig de beste glijhoek heeft. De verhouding horizontale snelheid/vertikale snelheid is hier optimaal. De glijhoek is simpelweg de verhouding tussen deze 2. Een glijhoek van 1:20 betekent dat je met 1 meter hoogteverlies 20 meter afstand af kunt leggen. Voor elk ander punt in de polaire is de verhouding horizontale/vertikale snelheid slechter.
Deze snelheid is interessant als je zoveel mogelijk lucht wilt doorkruisen, bijvoorbeeld tijdens het zoeken naar een bel. Als je vliegtuig deze snelheid vliegt kan hij met een gegeven hoogte zoveel mogelijk meters afleggen.
De snelheid voor beste glijhoek ligt meestal zo'n 20-30% hoger dan de snelheid voor minimum dalen. De daalsnelheid ligt echter veel minder dan 20-30% hoger, vandaar de toename in glijhoek. Bij deze snelheid gaat je zwever 'lopen'.
Als je nog sneller gaat vliegen blijft de glijhoek vaak redelijk op peil tot een gegeven snelheid, waarbij je een soort knik in de polaire ziet. In deze figuur zit een lichte knik, hoe erg de knik is hangt van het vliegtuig af. Bij oude zwevers is de knik veel erger (en bij een lagere snelheid) aanwezig dan bij moderne zwevers. Boven de snelheid waar die knik zit wordt het vliegtuig ineens minder efficient en wordt de glijhoek ineens rap slechter bij toenemende snelheid. Het is zaak beneden de vliegsnelheid van deze knik te blijven.
Nu gaan we eens kijken wat de invloed van wind is.

De rode polaire is de basis polaire zoals hierboven getekend, dus in stille lucht. Als we nu tegen wind in moeten gaan vliegen is de grondsnelheid lager dan de vliegsnelheid. De witte lijn is de polaire tov de grond als je tegen wind in vliegt. Hoe meer wind, hoe meer de polaire opschuift.
Nu wil ik weten wat de invloed van die wind is op de glijhoek tov de grond.

Uit deze figuur zijn 2 belangrijke conclusies te trekken.
1) De glijhoek tov de grond in tegenwind is slechter dan zonder wind.
2) De vliegsnelheid waarbij de beste glijhoek tov de grond wordt gehaald is hoger dan zonder wind. De raaklijn ligt nl op een punt verder langs de kromme, dus bij een hogere vliegsnelheid.
Stel je nu het volgende voor: je bent in een matige bel geklommen, en ondertussen is je vliegtuig door de wind benedenwinds geraakt. Nu wil je naar jezelf terugvliegen. Dat wil je doen met de beste glijhoek tov de grond. Veel mensen hebben de natuurlijke neiging de neus omhoog te trekken, omdat ze het vliegtuig anders zo hard zien zakken. Dat is nu net niet goed! Als je langzamer gaat vliegen neemt de glijhoek tov de grond drastisch af. Je moet juist wat sneller gaan vliegen. Ja, je vliegtuig zakt dan wat harder, maar hij gaat ineens ook veel beter vooruit komen, waardoor je toch beter terugkomt.
Bij meewind schuift de polaire de andere kant op. Het effect is dan dat de vliegsnelheid voor beste glijhoek wat afneemt, maar het verschil is veel kleiner dan bij tegenwind. Bij meewind voldoet in de praktijk de snelheid voor minimum daalsnelheid goed.
De invloed van stijgende / dalende lucht.
Stel nu dat je door een stuk lucht vliegt dat daalt.

De rode lijn is weer de oorspronkelijke polaire, de witte is de polaire in de dalende lucht. We zien nu dat de beste glijhoek tov de grond in dalende lucht bij een hogere vliegsnelheid ligt dan in stille lucht. Dat betekent dat je ook in dalende lucht beter wat harder kunt gaan vliegen. Ook hier voelt het onnatuurlijk aan omdat je door harder te gaan vliegen de daalsnelheid verder toe laat nemen, en die is al zo hoog in de dalende lucht. Maar toch kom je wel beter vooruit waardoor je eerder door het daalgebied heen bent.
Bij stijgende lucht schuift de polaire de andere kant op:

Ik heb hier de raaklijn vanuit de oorsprong aan de polaire ingetekend, maar eigenlijk is de snelheid die hierbij hoort niet interessant. Deze geeft nl de beste stijghoek tov de grond. Maar in een bel ga je draaien en is de stijghoek niet belangrijk. Het is belangrijker dat je zo snel mogelijk omhoog komt. En dat doe je met de snelheid waarbij de eigen daalsnelheid van het vliegtuig minimaal is. Als je langzamer gaat vliegen dan deze snelheid zit je bovendien erg dicht bij de overtrek. De invalshoek tijdens vliegen in thermiek verandert nogal door turbulentie in de bel, dus je wilt niet te langzaam vliegen, anders heb je de helft van de tijd loslatende stroming op je vleugel. Weg efficientie....
Laatst bewerkt door een moderator: