zonnepanelen op dak ; ja of nee
- Topicstarter Baggeraar
- Startdatum
prop-er
Forum veteraan
De invloed van de buitentemperatuur is anders aanzienlijk hoor!
Dit kan zomaar 10 tot 20% in vermogen schelen.
http://nl.wikipedia.org/wiki/Zonnepaneel:
Dit kan zomaar 10 tot 20% in vermogen schelen.
http://nl.wikipedia.org/wiki/Zonnepaneel:
Uit mijn type blad:
Temperature Characteristics
Nominal Operating Cell Temperature (NOCT) 45±2°C
Temperature Coefficient of Pmax -0.45 %/°C
Heb mijn panelen nooit gemeten met de volle zon erop.
Het lijkt me dat ze uitgaan van 45° voor het opgegeven vermogen.
Als ik het goed begrijp heb je bij een paneel temperatuur van 60° dan een mogelijke vermindering in opbrengst van 6.75°
Temperature Characteristics
Nominal Operating Cell Temperature (NOCT) 45±2°C
Temperature Coefficient of Pmax -0.45 %/°C
Heb mijn panelen nooit gemeten met de volle zon erop.
Het lijkt me dat ze uitgaan van 45° voor het opgegeven vermogen.
Als ik het goed begrijp heb je bij een paneel temperatuur van 60° dan een mogelijke vermindering in opbrengst van 6.75°
Die temp verandering tov opbrengst is waarschijnlijk afhankelijk van het merk en type panelen
prop-er
Forum veteraan
Ik ben ook wel benieuwd hoe dit werkt, dus heb ik het uitgezocht.
Wp:
Het piekvermogen van de panelen is bekend. Dit is het vermogen dat de cel levert bij STC. (Standard test conditions) = instraling 1000W/m², Module temperature 25°C, air Mass 1,5.
NOCT
Naast dit piekvermogen bij STC is er ook een NOCT, oftewel "Nominal Operating Cell Temperature" = De temperatuur van een paneel bij een instraling van 800 W/m² en een buitentemperatuur van 20°C en een windsnelheid van 1m/s bij een opstelhoek van 45°.
De NOCT van mijn panelen is 45°C, dus identiek aan die van jou.
δ Temperature Coefficient:
Dit is de verandering in vermogen voor een andere temperatuur dan 25°C. Deze bedraagt bij mij ook 0,45%/°C.
Om iets zinnigs over het vermogen bij diverse buitentemperaturen te kunnen zeggen, is het van belang de bijbehorende paneeltemperatuur te weten.
Die kan als volgt berekend worden:
Tpv = Tbuiten + S / 800 * (TNOCT - 20)
De buitentemperatuur is momenteel zo'n 0°C.
De zonnestraling S is de afgelopen dagen zo'n 400 W/m² geweest.
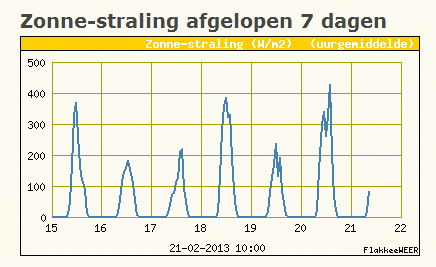
Bron: Actuele zonne-straling
Omdat dez straling horizontaal gemeten wordt, kan de straling op de panelen die onder een hoek van 30° opgesteld staan zo'n 50% hoger uitvallen. (Bron: http://www.knmi.nl/klimatologie/achtergrondinformatie/Zonnestraling_in_Nederland.pdf) Laten we aldus een waarde van 600 W/m² aannemen.
Tpv = 0°C + 600/800 * (45°C - 20°C) = 18.75°C
Gevoelsmatig lijkt me dat aan de hoge kant. Aangezien de gevoelstemperatuur met de harde wind van de afgelopen dagen zomaar 8° lager kan liggen, hou ik voor de panelen een werktemperatuur van 10°C aan.
Daarmee kan het werkelijke vermogen berekend worden:
Wpv = Wp * S / 1000 * [1 - δ * (Tpv - 25)]
Wpv = 225 * 600/1000 * (1 - 0,0045 * (10°C - 25°C) = 144Wp
Voor mijn 16 panelen is dat totaal zo'n 2300Watt. Daar zit ik gisteren met 3450W ruim boven!
Klopt de formule wel?
In deze sheet staan de specificaties van mijn panelen LDK225P: http://www.ldksolar.com/uploadfiles/down/LDK_DS_235P-20_value_EN_V3_120817.pdf
Power Output (Pmax) [W] bij NOCT (800W/m² & 45°C) = 164W
Even narekenen:
Wp * S / 1000 * [1 - δ * (Tpv - 25)] = Wpv
225 * 800/1000 * [1- 0.0045 * (45-25)] = 164W
De formule klopt exact met de opgave van de fabrikant.
De temperatuur heeft een vrij kleine invloed op de resultaten. Bij een extreem lage paneeltemperatuur van 0°, misschien mogelijk doordat de straling kort daarvoor nog niet voldoende sterk was om het paneel op te warmen, is de invloed op het vermogen maar zo'n 10%. Om de gemeten 215W per paneel te halen, moet de straling dus zomaar even 860 W/m² geweest zijn. Volgens mij is dat vrijwel onmogelijk, en ik vermoed dat deze piekmeting niet correct is. Bij andere installaties zie ik de afgelopen dagen ook een piekvermogen van ongeveer 2/3 van Wp ontstaan, wat met de berekening overeen komt.
Ik zal er eens mijn logs op moeten naslaan om te zien wat er mis gaat.
Stel nu dat we in de zomer de 30°C aantikken, bij een straling van 1200W/m².
Tpv = 30°C + 1200/800 * (45°C - 20°C) = 61°C
Wpv = 225 * 1200/1000 * (1 - 0,0045 * (67,5°C - 25°C) = 218Wp
Je ziet hier dat de forse werktemperatuur van de panelen de resultaten met zomaar even 20% nadelig beïnvloeden.
Bij een extreem lage werktemperatuur van 0° wordt het resultaat met 10% positief beïnvloed.
Het uiteindelijke vermogen wordt echter ook bepaald door de instraling, die in de winter beduidend lager is dan in de zomer.
Ik hoop dat het zo iets duidelijker is...
Je ziet ook dat het best lonend kan zijn om de panelen in de zomer te koelen met water, mits je dat eenvoudig en goedkoop beschikbaar hebt natuurlijk.
Wp:
Het piekvermogen van de panelen is bekend. Dit is het vermogen dat de cel levert bij STC. (Standard test conditions) = instraling 1000W/m², Module temperature 25°C, air Mass 1,5.
NOCT
Naast dit piekvermogen bij STC is er ook een NOCT, oftewel "Nominal Operating Cell Temperature" = De temperatuur van een paneel bij een instraling van 800 W/m² en een buitentemperatuur van 20°C en een windsnelheid van 1m/s bij een opstelhoek van 45°.
De NOCT van mijn panelen is 45°C, dus identiek aan die van jou.
δ Temperature Coefficient:
Dit is de verandering in vermogen voor een andere temperatuur dan 25°C. Deze bedraagt bij mij ook 0,45%/°C.
Om iets zinnigs over het vermogen bij diverse buitentemperaturen te kunnen zeggen, is het van belang de bijbehorende paneeltemperatuur te weten.
Die kan als volgt berekend worden:
Tpv = Tbuiten + S / 800 * (TNOCT - 20)
De buitentemperatuur is momenteel zo'n 0°C.
De zonnestraling S is de afgelopen dagen zo'n 400 W/m² geweest.
Bron: Actuele zonne-straling
Omdat dez straling horizontaal gemeten wordt, kan de straling op de panelen die onder een hoek van 30° opgesteld staan zo'n 50% hoger uitvallen. (Bron: http://www.knmi.nl/klimatologie/achtergrondinformatie/Zonnestraling_in_Nederland.pdf) Laten we aldus een waarde van 600 W/m² aannemen.
Tpv = 0°C + 600/800 * (45°C - 20°C) = 18.75°C
Gevoelsmatig lijkt me dat aan de hoge kant. Aangezien de gevoelstemperatuur met de harde wind van de afgelopen dagen zomaar 8° lager kan liggen, hou ik voor de panelen een werktemperatuur van 10°C aan.
Daarmee kan het werkelijke vermogen berekend worden:
Wpv = Wp * S / 1000 * [1 - δ * (Tpv - 25)]
Wpv = 225 * 600/1000 * (1 - 0,0045 * (10°C - 25°C) = 144Wp
Voor mijn 16 panelen is dat totaal zo'n 2300Watt. Daar zit ik gisteren met 3450W ruim boven!
Klopt de formule wel?
In deze sheet staan de specificaties van mijn panelen LDK225P: http://www.ldksolar.com/uploadfiles/down/LDK_DS_235P-20_value_EN_V3_120817.pdf
Power Output (Pmax) [W] bij NOCT (800W/m² & 45°C) = 164W
Even narekenen:
Wp * S / 1000 * [1 - δ * (Tpv - 25)] = Wpv
225 * 800/1000 * [1- 0.0045 * (45-25)] = 164W
De formule klopt exact met de opgave van de fabrikant.
De temperatuur heeft een vrij kleine invloed op de resultaten. Bij een extreem lage paneeltemperatuur van 0°, misschien mogelijk doordat de straling kort daarvoor nog niet voldoende sterk was om het paneel op te warmen, is de invloed op het vermogen maar zo'n 10%. Om de gemeten 215W per paneel te halen, moet de straling dus zomaar even 860 W/m² geweest zijn. Volgens mij is dat vrijwel onmogelijk, en ik vermoed dat deze piekmeting niet correct is. Bij andere installaties zie ik de afgelopen dagen ook een piekvermogen van ongeveer 2/3 van Wp ontstaan, wat met de berekening overeen komt.
Ik zal er eens mijn logs op moeten naslaan om te zien wat er mis gaat.
Stel nu dat we in de zomer de 30°C aantikken, bij een straling van 1200W/m².
Tpv = 30°C + 1200/800 * (45°C - 20°C) = 61°C
Wpv = 225 * 1200/1000 * (1 - 0,0045 * (67,5°C - 25°C) = 218Wp
Je ziet hier dat de forse werktemperatuur van de panelen de resultaten met zomaar even 20% nadelig beïnvloeden.
Bij een extreem lage werktemperatuur van 0° wordt het resultaat met 10% positief beïnvloed.
Het uiteindelijke vermogen wordt echter ook bepaald door de instraling, die in de winter beduidend lager is dan in de zomer.
Ik hoop dat het zo iets duidelijker is...
Je ziet ook dat het best lonend kan zijn om de panelen in de zomer te koelen met water, mits je dat eenvoudig en goedkoop beschikbaar hebt natuurlijk.
Laatst bewerkt:
prop-er
Forum veteraan
Dat valt dus mee.
Poly's en mono's zitten over het algemeen tussen de -0,44 en -0,50 %/°C
Er zijn echter ook enkele panelen die fors lager zitten (-0,34 tot -0,38 %/°C)
Dat geldt alleen voor levende dingen.
De rest van je verhaal zal ik vanavond eens door lezen.
Jullie maken er nog al een rekenwerk van.
Ik kijk alleen naar de teller wat hij opwekt.
Hoe dat gebeurd is voor mij niet zo belangrijk haha.
Berrie schaduw op een klein stukje van een paneel schijnt al pittige gevolgen te hebben voor alle panelen.
Als ik het goed begreep trek je met een klein stukje schaduw alle panelen mee.
Maar op jou dakkapel kunnen toch wel een paar panelen.
Als je er 3 op zet heb je toch een opbrengst van zo'n 600 kWh.
Onder het motto beter iets dan niets.
Ik kijk alleen naar de teller wat hij opwekt.
Hoe dat gebeurd is voor mij niet zo belangrijk haha.
Berrie schaduw op een klein stukje van een paneel schijnt al pittige gevolgen te hebben voor alle panelen.
Als ik het goed begreep trek je met een klein stukje schaduw alle panelen mee.
Maar op jou dakkapel kunnen toch wel een paar panelen.
Als je er 3 op zet heb je toch een opbrengst van zo'n 600 kWh.
Onder het motto beter iets dan niets.
Als je last hebt van schaduw kun je in sommige omvormers opti-track aanzetten, dit kost wat vermogen, maar levert bij schaduw werking toch meer op.
Let op: aanpassingen in de omvormer zijn voor eigen risico.
Let op: aanpassingen in de omvormer zijn voor eigen risico.
ja of nee,
nee hier in zeeland bij de Delta heeft mijn vader uit gerekend, dat het van de delta goedkoper is dan zonnepanelen
nee hier in zeeland bij de Delta heeft mijn vader uit gerekend, dat het van de delta goedkoper is dan zonnepanelen
HAHA, ik heb een houtzaag gebruikt om te verhelpen wat ik zelf kon.
Huizen van de buren doe je niets tegen natuurlijk.
@Paul, zonnepanelen zijn leuk als je het geld er voor over hebt, energie kan alleen maar duurder worden.
En ooit (met een jaar of 8) heb ik mijn geld weer terugverdiend en na die tijd ga ik er aan verdienen.
Geen energiemaatschappij die dan mijn stroom goedkoper kan leveren.
((energiedirekt, budgetenergie, eon, nuon zijn bovendien (bij prizewize) goedkoper dan delta.))
Harm,
gaan die panelen 8 jaar mee?
en leveren ze dan nu nog even veel stroom?
afschrijfwaarde - gebruiksjaren
gaan die panelen 8 jaar mee?
en leveren ze dan nu nog even veel stroom?
afschrijfwaarde - gebruiksjaren
De levensduur van panelen is 30 jaar.
Ze lopen terug in opbrengst. Dit is middels garanties en eventueel verzekeringen vastgelegd.
Zo heb ik voor 5 jaar 95% - 98% gegarandeerd (weet het preciese getal niet uit mn hoofd)
Dan tot 12 jaar 90% en tot 25 jaar 80%.
Bij mijn panelen is dit via een verzekering van de fabrikant geregeld. Als het systeem kapot gaat binnen die tijd krijg ik 7.50 euro per dag tot het gerepareerd is.
Ze lopen terug in opbrengst. Dit is middels garanties en eventueel verzekeringen vastgelegd.
Zo heb ik voor 5 jaar 95% - 98% gegarandeerd (weet het preciese getal niet uit mn hoofd)
Dan tot 12 jaar 90% en tot 25 jaar 80%.
Bij mijn panelen is dit via een verzekering van de fabrikant geregeld. Als het systeem kapot gaat binnen die tijd krijg ik 7.50 euro per dag tot het gerepareerd is.
Bij een beschermd stadsgezicht of monumentaal pand kan ik me er iets bij voorstellen, maar kans heb je altijd.
Het moet wel je eigen dak zijn en je panelen moeten voor jouw gebruik zijn.
(je mag dus niet "je dak oppervlak verhuren aan derden")
Ik heb ze er gewoon op gelegd, de gemeente ziet maar. . .
Zelf laten ze monumentale panden compleet ruïneren door huurders die dan weer OZB en andere tax leveren in hun voordeel (dan mag werkelijk alles).
@Dirk hoe zit het met jullie rekening???
Het moet wel je eigen dak zijn en je panelen moeten voor jouw gebruik zijn.
(je mag dus niet "je dak oppervlak verhuren aan derden")
Ik heb ze er gewoon op gelegd, de gemeente ziet maar. . .
Zelf laten ze monumentale panden compleet ruïneren door huurders die dan weer OZB en andere tax leveren in hun voordeel (dan mag werkelijk alles).
@Dirk hoe zit het met jullie rekening???
Kun je niet een keertje bij mij langskomen met die super zaag van je.
wel zachtjes doen en 's nachts. Staan wat bomen in de weg :rolling:
LOL
Gelukkig had mijn overbuurman een vooruitziende blik en heeft die al het e.e.a. gerooid. Met bomen van de gemeente doe je helaas niet zoveel.