Servo inbouw .

Mark Oostveen zei:
Theo,

Ik vindt het lastig om het je duidelijk uit te leggen zonder een heel fundamenteel verhaal te beginnen over mechanica (de leer van krachten, momenten, sterkte doorbuigingen etc.).
De blauwe lijnen zoals jij ze getekend hebt zijn in iedergeval geen reactiekrachten in de servo veroorzaakt door het trekken aan de servo..

Je theorietje over het kantelen over een lange en kantelen over een kortelijn is interesant.. Dat is nu net waarop ik geprobeerd heb de theoretische onderbouwing van te geven. Het maakt dus niets uit of ik trek in de richting B over de lengte d, of in de richting A over de lengte c.

Hier een stukje uitleg. Een kanteling wordt veroorzaakt doordat een kracht aangrijpt op een ander punt dan het draaipunt. Dat moge duidelijk zijn, een kracht in een draaipunt verdraait niets. Doe de deur maar eens dicht door op het draaipunt te drukken... nou dan ben je nog wel even bezig :) .
Ik denk ook dat je het volgende weet en anders wel aan kunt voelen: Hoe verder de kracht van het draaipunt af staat (dat is de "arm") hoe meer moeite je moet doen in het draaipunt om draaien te voorkomen. Dit is het zelfde als: Het kost meer kracht om de de deur te sluiten als ik in de buurt van het draaipunt duw of als ik bij de klink duw. De weerstand in het scharnier moet overwonnen worden en dat kan dus op 2 manieren. De variatie is dat in beide gevallen de kracht vermenigvuldigd met de afstand naar het draaipunt gelijk is. Even een voorbeeld:

De deur is één meter breed. Bij de klink (1 meter van het draaipunt) moet ik met 2 kg drukken om de deur dicht te krijgen. Het door mij opgewekte "moment" is dan 2kgx1m = 2Kg/m (2kg per meter). Als ik nu op 0.1 meter ga drukken dan moet ik om datzelfde moment
op te brengen dus met 20kg drukken. 20kgx0.1m=2kg/m

Dit is eigenlijk de hele basis van mijn betoog. Het enige is dat we van mening verschillen over wat nu de "arm" is die de afstand definieerd tussen de kracht en het draaipunt. De definitie uit de mechanica is:

De arm is de loodrechte afstand van de kracht naar het draaipunt.

Dit is exact wat ik gedaan heb. Mijn arm a staat haaks op de kracht Fr. Jouw arm c staat niet loodrecht op de kracht a.. Daar zit het verschil.

En omdat ik het niet met woorden kan vertellen, hier het bewijs.

normal_Arm_recht_boven_draaipunt.jpg


Arm_verschoven_tov_draaipunt.jpg


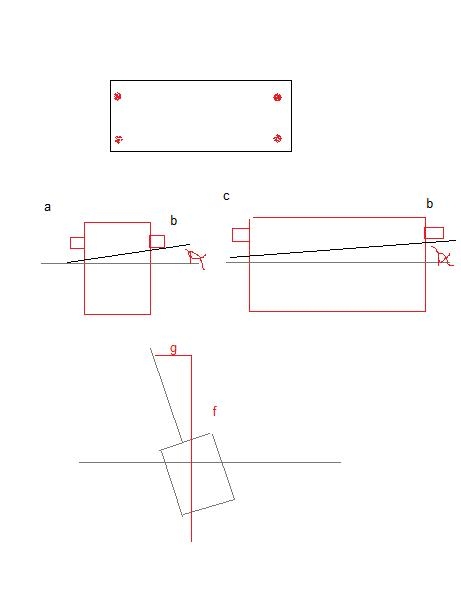
Achterste balk horizontaal: Dit is de wip
Rode pijl: Daar zit het draaipunt
Beide schroeven even hoog boven de wip uit.
Bovenste foto is als de deur. Je trekt recht boven het draaipunt.
Onderste foto is als servo. Je trekt verschoven t.o.v. draaiunt.

En je ziet de reactiekracht door de weegschaal gemeten is in beide situaties gelijk (2764 gram en 2753 gram).

Grz

mark
Klik om te vergroten...

Zolang je geen maat van kracht weergeeft op je draad, bewijs je nog niet echt iets...maar we zullen aannemen dat die in beide gevallen gelijk was. :)

En deze proef was dan ook correct tot dat...je een kanteling krijgt, in dat geval zal de arm in het eerste plaatje niks tot weinig veranderen, dus je moment blijft ongeveer hetzelfde. In je tweede plaatje daarentegen zal de kop van je schroef stijgen en daarmee ook je arm verlengen, met dezelfde kracht maal een langere arm, krijg je een groter moment.
 
Ik ben het op 1 punt gewoon nog steeds niet eens met de momentplaatjes. Er wordt in de plaatjes van een Fs (zie plaatjes) uitgegaan die recht omhoog gaat vanuit het achterste bevestigingspunt. Dit is gewoon niet waar. Er is ook een kracht omlaag in het voorste bevestigingspunt. Die kun je gewoon zien als je aan een servo trekt, hij komt aan de achterkant omhoog en gaat aan de voorkant omlaag.

Dat is ook wat er niet goed is aan de momentheorie. Die gaat er nameljik van uit dat de servo vast zit en niet kan bewegen. Dit is echter niet waar. De servo kan wel degelijk bewegen, wat in de 1e post van dit topic al heel duideiljk aangetoond wordt.

Het model wat hier gepresenteerd wordt is dus niet volledig en daarmee incorrect. Het is de weergave van het moment in de tijd dat de servo de volledige beweging gemaakt heeft en de eindpunten van deze beweging bereikt heeft. Het zou mij niets verbazen als in het bewegende stuk de situatie anders in elkaar zit. Instinctief zeg ik hetzelfde als Theo, maar ik heb even niet de zin om de weggezakte natuurkundekennis weer op te gaan poetsen hiervoo.. ;)
 
En deze proef was dan ook correct tot dat...je een kanteling krijgt,
Klik om te vergroten...

Hier gaat het niet om een kanteling die niet gaat komen .

Gaat alleen om de kracht op de schroefen bij servo inbouw en die blijft gelijk als het servo 180° gedraait word . ;)

Mark hat ook de schroef nog een meter verder terug kunnen zetten . :D

Mvg Johan
 
Nou Hezik vooruit dan,

Je hebt gelijk. :) Nee even serieus, ik zit je niet te pesten.

Fs is de kracht in de schroef aan de rechter zijde. Deze kracht (vertikaal) wordt volledig opgewekt door de kracht van het roer Fr en dan de momentenstelling.

Echter zoals je al eerder terecht opmerkte is er meer dan alleen "som van de momenten = 0" je hebt ook nog "som van de krachten = 0" en om het verhaal compleet te maken zou je die daarna ook nog moeten beschouwen.

Dus Fs opgewekt door het moment houdt de servo beneden. Dat betekend dat er een even grote kracht de servo omhoog moet houden om te voorkomen dat de servo er vandoor gaat. Dus inderdaad aan de linkerkant staat het plankje de servo tegen te houden met een kracht die gelijk is aan Fs zoad in vertikale richting de "som van de krachten 0 is"

Horizontaal moet je dat dan ook nog doen. En dat betekend dat er links en rechts bij de schroeven een horizontale kracht komt te staan van 0.5xFr naar rechts, beide zijden vangen de helft op.

En dan is het plaatje compleet

krachten_servo_2.jpg


Dat is ook wat er niet goed is aan de momentheorie. Die gaat er nameljik van uit dat de servo vast zit en niet kan bewegen. Dit is echter niet waar. De servo kan wel degelijk bewegen, wat in de 1e post van dit topic al heel duideiljk aangetoond wordt.
Klik om te vergroten...

Klopt niet helemaal. De momentenstelling en de krachtenstelling gaan uit van evenwicht (dat zegt de = 0). Een rust situatie, dat moet ook, zou er geen evenwicht zijn dan zou de servo door blijven bewegen. Dus niet een beetje en dan stoppen, nee continu door bewegen.
Ik zal de beredenering rond maken. De bewegingen die Herr Plotterwelt :) op de foto heeft gezet die komen ergens vandaan. Dat moet komen omdat er krachten werken op de servo. Een rubberen tulle waarin de servo hangt is een veer. Hoe harder ik druk hoe verder ik hem inknijp. En daar zit de truuk.

Ik beweer met mijn momentenstelling dat je de servo het beste in de lengterichting kunt plaatsen (ongeacht de uitgaande as links of rechts) omdat dan de krachten op de schroeven (oftewel de rubberen tulles) het kleinste zijn. Als de krachten op de tulles klein is zal ook de beweging die die tulle de servo toestaat klein zijn (kleine kracht, kleine indrukking, grote kracht, grote indrukking). --> zie hier het bewijs in de foto's van plotterwelt
 
Laatst bewerkt:
hezik zei:
Dat is ook wat er niet goed is aan de momentheorie. Die gaat er nameljik van uit dat de servo vast zit en niet kan bewegen. Dit is echter niet waar. De servo kan wel degelijk bewegen, wat in de 1e post van dit topic al heel duideiljk aangetoond wordt.
Klik om te vergroten...


In dat geval spreekt men van een koppel en niet van een moment. Moment- theorie houd wel rekening met andere inwerkende krachten.
 
hezik zei:
Ik ben het op 1 punt gewoon nog steeds niet eens met de momentplaatjes. Er wordt in de plaatjes van een Fs (zie plaatjes) uitgegaan die recht omhoog gaat vanuit het achterste bevestigingspunt. Dit is gewoon niet waar. Er is ook een kracht omlaag in het voorste bevestigingspunt. Die kun je gewoon zien als je aan een servo trekt, hij komt aan de achterkant omhoog en gaat aan de voorkant omlaag.

Dat is ook wat er niet goed is aan de momentheorie. Die gaat er nameljik van uit dat de servo vast zit en niet kan bewegen. Dit is echter niet waar. De servo kan wel degelijk bewegen, wat in de 1e post van dit topic al heel duideiljk aangetoond wordt.

Het model wat hier gepresenteerd wordt is dus niet volledig en daarmee incorrect. Het is de weergave van het moment in de tijd dat de servo de volledige beweging gemaakt heeft en de eindpunten van deze beweging bereikt heeft. Het zou mij niets verbazen als in het bewegende stuk de situatie anders in elkaar zit. Instinctief zeg ik hetzelfde als Theo, maar ik heb even niet de zin om de weggezakte natuurkundekennis weer op te gaan poetsen hiervoo.. ;)
Klik om te vergroten...

Er is geen kracht naar beneden op het draaipunt , hij zakt iets door het rubbertje naar beneden , denk de rubbers maar effe weg .

Heb het hele gedoe van krachten ,momenten en hevels voor 5 jaar nog eens op school gehat , boeken liggen hier ook nog . :D
Zit alles nog fris in mijn hoofd .

Mvg Johan
 
Hij zakt door het rubbertje naar beneden. Dan kun je lang lullen en kort lullen, maar dan is er dus een kacht. Zonder een kracht geen beweging. Het feit dat hij in het rubbertje zakt, is gewoon bewijs dat er een kracht is.

De rubbers mag je dus NIET wegdenken, dat is juist mijn punt. Jullie gaan van een statische situatie uit, terwijl de situatie niet statisch is. Bekijk nou nog even de foto's uit je eigen topicstart en zie hoe alles beweegt. Was die beweging er niet geweest, dan had je gelijk gehad.

Helemaal nitwit ben ik niet, ik heb 2 jaar Werktuigbouw gestudeerd aan de UT, alleen door inloting bij een andere studie mee gestopt ;)
 
Hezik,

heb je nu mijn bericht gelezen.

Ja er is daar een kracht naar beneden die wordt tegengehouden door de plank..

Zie mijn laatste bericht, en reageer daar eens op.
 
Ok ik wil er wel op reageren.

Jij schrijft de mindere uitslagen zoals gedemonstreerd op de foto's van johan, toe aan het vermeend minder zijn van de krachten en daardoor kleinere beweging in de rubbers.

Dat is niet zo. Er is eenzelfde beweging in de rubbers maar doordat de bevestigingspunten dichter bij elkaar staan, is de hoek groter.

Ik ga dit even uittekenen om duidelijk te maken wat ik bedoel.
 
Ik heb op deze pc alleen paint, dus geen mooie tekening, maar het moet maar even zo.

5381480cf3e76aa2f.jpg


Ik heb eerst even de servo van boven getekend. Je ziet de 4 bevestigingspunten.

Daaronder staat links de servo die scheefgedrukt staat in de lengterichting, rechts de servo die scheefgedrukt staat in de breedterichting. Daaronder staat een servo zoals Johan 'm in de startpost had, met de rode lijnen geef ik de hartlijn en de afwijking ten opzichte van de oorspronkelijke positie aan.

Omdat ik neit weet hie je met paint scheve vierkanten tekent, heb ik in de middenste tekening niet de servo scheef gezet, maar even het opperlvlakte waar die servo in staat geheld. Dat maakt voor het verhaal niet uit, het gaat er om dat de servo een hoek maakt ten opzichte van het platte vlak waar hij in staat.

Goed.. we beginnen even met de onderste tekening. Ik ga dat niet helemaal uitwerken met wiskunde, ik denk dat uit de tekening wel al duidelijk wordt dat hoe groter de hoek is die de servo maakt met het plakke vlak, hoe groter de afwijking die de arm maakt ten opzichte van de 'in rust' positie.

Dan doe ik 1 aanname waarvan ik denk dat je die veilig kunt maken, namelijk dat elk bevestigingspunt evenveel speelruimte heeft in het rubbertje. Voor het gemak ga ik even uit van 1mm speling, die afstand is in feite arbitrair voor wat we willen vergelijken.

We pakken nu de servo die in lengterichting (dus 'goed' ) gemonteerd zit. Het voorste bevestigingspunt zakt 1 mm naar beneden, het achterste punt 1 mm omhoog. Voor de berekening van de hoek kunnen we ook zeggen dat het voorste punt blijft waar het is, maar het achterste punt 2mm omhoog gaat.

Dan rekenen we de hoek uit die de servo maakt ten opzichte van het grondvlak. Stel dat de servo in lengterichting 3cm is. We weten dan het aanliggende en het overstaande been van de zo gevormde driehoek. We dienen dus de tangens te gebruiken.

De tangens van de hoek is dan dus de overstaande zijde gedeeld door de aanliggende, oftewel 2/30 (we doen het in mm). De rekenmachine leert je dan dat de hoek die de servo maakt, 3.8 graden is.

Stel we doen dit nu voor de andere situatie, waarin de servo zijdelings belast wordt. Stel dat de servo 1cm breed is. De tangens van de hoek is dan 2/10, wat volgens de rekenmachine een hoek van 11 graden.

De servo kan, met dezelfde speling op de rubbers, in een zijdlings geplaatste situatie dus een grotere hoek maken ten opzichte van het vlak waar hij zich in bevind. Dat is hiermee wiskundig aangetoond.

Uit het 3e plaatje hadden we geconcludeerd dat een grotere hoek automatisch ook een grotere afwijking betekende.

De grotere afwijking komt dus niet door grotere of kleinere krachten danwel momenten, maar domweg door de geometrie van het geheel.

De beweging in de rubbers is dus voor hetgeen geconstateerd in de topicstart de enige en ook enige juiste verklaring.

De 2e discussie gaat dan over de krachten op de schroefjes. Dat staat geheel los van hetgeen in de topicstart gedemonstreerd. Het feit dat er sprake is van beweging, die gewoon met de blote ogen waar te nemen is en ook duidelijk gedemonstreerd is in de foto's in de topicstart, kun je domweg neit zeggen dat er op het kantelpunt geen kracht werkt. Immers dit punt is verplaatst dus heeft er een kracht gewerkt.

De gehele uitwerking van de krachten op de schroefjes zou dus ook in 2en gesplitst moeten worden. Als eerste is er een eenparige beweging waarbij de servo beweegt tot de maximale uitslag in de rubbers bereikt is. Het 2e gedeelte is dan een momentberekening, daar de servo op dat moment vast staat, de rubbers geven niet meer rek.

Stel nu eens we geven een korstondige ruk aan een servo. Hij zal dan in eerste instantie meebewegen, hij bouwt dus energie op. Op het moment dat de servo stil komt te staan, komt er dus energie vrij die eerder in de vorm van beweging aanwezig was. De geometrie van het geheel, het feit dat het makkelijker is om een schroef UIT het hout te rukken dan een servo erin te duwen, geeft aan dat, indien er sprake is van falen, dat falen eerder zal gebeuren als het draaipunt van de servo zich aan de korte kant bevind.

Ik denk dan ook dat daar de denkfout gemaakt word. Jullie gaan uit van een statische situatie met vaste krachten, echter we hebben het over een impulssituatie. Gevoelsmatig zeg ik dan ook dat Theo met zijn wijsheid over hoe een servo gemonteerd moet worden, gelijk heeft.

Hij geeft er immers ook bij aan dat het gaat over het 'uit het hout rukken' van de servo, als het ware. Dan is er dus geen sprake van een statische momentsituatie.
 
Laatst bewerkt door een moderator:
Nu ik er langer over nadenk, durf ik zelfs te poneren dat het meeste falen niet zal optreden in 'de momentsituatie' maar in de 'impulssituatie'. Dus als een servo energie heeft opgebouwd door een beweging die bij een plotseling stoppen (want eindpunt rubber bereikt) vrijkomt. In die situatie is de arm van de kracht wel degeljik groter als de servo het dichts bij het roer gemonteerd zit met de hevel.
 
Een servo kan geen energie opbouwen , alleen afgeven.

Een benzin motor bouwt energie op door een vertikale beweging (zuiger) om te zetten in een draaibeweging (krukas)
De energie zit dan in de gewichten op de krukas , vliegwiel of bv. propellor .

Goed voorbeeld is de 1 zilinder Lanz diesel die zonder het vliegwiel nooit kan lopen , de energie in het vliegwiel moet de zuiger weer over het bovenste punt drukken om opnieuw een ontsteking te krijgen .

Mvg Johan
 
Op het moment dat een servo beweegt in z'n rubbers, bouwt hij kinetische energie op. Dat is gewoon een natuurkundige wet.

Maar de rest van het verhaal geen reactie op?
 
Laatst bewerkt door een moderator:
Jongens hou nou eens op met gewoon natuurkundige wetten in twijfel te trekken. Iets wat beweegt heeft bewegingsenergie, dat is geen discussiepunt maar gewoon een feit, pak anders je natuurkundeboeken er nog eens bij en zoek het hoofdstuk kinetische energie eens op. En in de topicstart is al bewezen dat een servo beweegt.

Of die energie dan zo klein is dat hij verwaarloosbaar is, is een tweede. Dat zouden we moeten berekenen.. en daar heb ik vooralsnog geen zin in :P
 
Laatst bewerkt door een moderator:
Zo, dit begint nu een leuke en leerzame discussie te worden. Ik heb nog een oude (kapotte) servo liggen, Ik zal van de week eens serieus gaan testen wat nu beter is. Ik heb nog een kleine veerunster liggen die gaat tot 1 kilo, die zal ik dan gebruiken om de trekkrachten te meten.

Nog steeds ben ik niet overtuigd.
 
hezik zei:
Jongens hou nou eens op met gewoon natuurkundige wetten in twijfel te trekken. Iets wat beweegt heeft bewegingsenergie, dat is geen discussiepunt maar gewoon een feit, pak anders je natuurkundeboeken er nog eens bij en zoek het hoofdstuk kinetische energie eens op. En in de topicstart is al bewezen dat een servo beweegt.

Of die energie dan zo klein is dat hij verwaarloosbaar is, is een tweede. Dat zouden we moeten berekenen.. en daar heb ik vooralsnog geen zin in :P
Klik om te vergroten...

Voor kinetische energie heb je masse voor nodig .
Ben wel benieuwt hoe jij dit gaat uitrekenen .

Misschien moeten wetten nieuw geschreven worden .

Mvg Johan
 
Nee hoor johan.

We hebben het over een rotatiebeweging van een massa. De energie is dan uit te rekenen met:
5ba35e27382ebd9d237be50c81b8e14f.png


waarin I het traagheidsmoment van het roterende object is, in kg m² en ω de hoeksnelheid, in radialen per seconde.

Je wil toch niet zeggen dat jij gewichtsloze servo's in jouw toestellen hebt zitten? Zo wel, waar koop je die dan?

Het traagheidmoment kun je vinden met de formule:
9fd32dc65d7482224c8098880adf2f18.png


Waarbij het erg van belang is te noteren dat r in dit geval de loodrechte afstand is tot het draaipunt.

Dus de LOODRECHTE afstand, wat zou inhouden dat Theo toch gelijk heeft...
 
Laatst bewerkt door een moderator:
Heb je de foto's in de topicstart ook bekeken, charlie? Dit hele topic gaat er nu juist over dat de servo's wel bewegen..
 
You must log in or register to reply here.
Back
Top