DIT IS om te fluisteren, leer rekenen
Doe het eens voor .
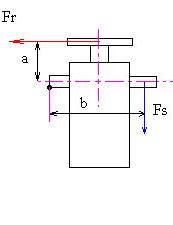
De rode krachten moeten ervoor zorgen dat de servo op zijn plek blijft (F mount).
In situatie 1 moet het moment gegenereerd door Fr opgevangen worden door krachten die een afstand B uit elkaar staan. In situatie 2 is die afstand A (beduidend langer!!) hier door zijn de afzonderlijke krachten (Fm 2L en Fm2R) kleiner dan die in situatie 1. Het balsa kan natuurlijk beide krachten hebben (we gingen er van uit dat de servo aan de 'aarde' zat) maar balsa veert veel (stijfheid is laag).
Daar klopt niet veel van wat je daar schrijft .
Mvg Johan
Laatst bewerkt: